配線の偏微分方程式

遅延が距離の2乗に比例するとか。
信号が波として伝わるとか。
反射するとか。

なんだか、良く分からない話が多い。
それが、配線というやつです。
回路図の上では、ただの線なのに･･･ですよ！

その原因はこれ。

配線には、色々な寄生成分があるからです。
直列に、抵抗RとインダクタンスLがあります。
並列に、コンダクタンスGと容量Cがあります。
これらは確かに小さいですが、決してゼロではありません。

こいつの一部の微小区間を取り出すと。

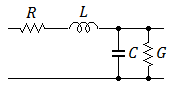
で、これの左端に電圧を加えたとき、右端に電圧が生じます。
が、途中の色んな成分で遅延やらなんやらが生じます。
それを記述する配線の偏微分方程式というのが、今回のテーマ。

左端から右端までの間には距離xがあります。
信号が伝わる間には時間tがあります。
この二つの変数でもって、偏微分方程式を記述します。

まず電圧について。

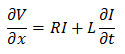
そして、電流について。

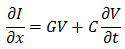
この二つの式を代入して合体させると以下の偏微分方程式になります。

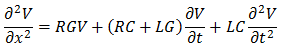
このままじゃ複雑すぎるので、少しずつ近似していきます。
まずコンダクタンス成分Gは鬱陶しいので無視します。
配線からグラウンドに、そう簡単に電流が流れちゃ困るって話です。

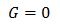
そして得られた方程式がこれ。

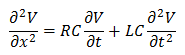
正確には、この方程式を使うべしです。
でも、配線によっては更にインダクタンスが無視できたり、抵抗が無視できたりします。

LSIチップの上の配線、つまりオンチップではインダクタンス成分が無視できます。
オンチップの配線はめちゃくちゃ細いから、抵抗は大きいです。
それに対してインダクタンスが無視できるのは、チップが小さいだけに配線も短いからです。

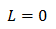
すると、配線の方程式は、「拡散方程式」というやつになります。

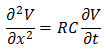
一方、オフチップでは抵抗成分が無視できます。
オフチップの配線は長いからインダクタンス成分が大きい。
配線自体は太いから抵抗は小さいですよね。
さっきの逆です。

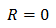
すると、今度は「波動方程式」になります。

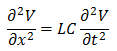
･･･というわけで、オンチップの信号は拡散的に伝わります。
オフチップの信号は波動として伝わります。

そういうわけで、状況によって信号の伝わり方には随分差があります。
状況に応じて、遅延の対策も変えなきゃいけないってことでしょうね。

拡散方程式を解けば分かりますが、オンチップでは距離の2乗に比例して遅延が生じます。
だから配線は短く、短く。

オフチップでは信号は波として伝わるので、反射を避けなければなりません。
いちいち反射されてちゃ、なかなか信号が伝わっていかないからです。
そんなわけで、インピーダンス整合なんてことを考えるべしっていうことになります。