3つ目のパターンとして基底を次の様にとります。
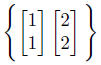
正確にはこれを基底と呼んではいけないのだけど、ここでは目を瞑ることにします。
りんごとみかんの1個ずつのセットと、2個ずつのセットが売られているパターンです。
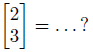
このパターンでしか売られていない場合、りんご2個とみかん3個が欲しい場合はどうしよう?
どうにもできません。
今までの2つの基底なら良くて、今度の基底がダメな理由は何か?
それは、ベクトルが「一次独立」か「一次従属」かです。
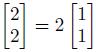
今回、基底とした2つのベクトルの間には、このような関係があります。
このような関係が存在することを「一次従属」と言います。
ベクトルが2個あれば、2次のベクトルを全て表わし尽くせると言いました。
が、この従属関係があると、ベクトルが実質的に1個に見えてしまいます。
そういうわけで、2次のベクトルの全てを表すことはできません。
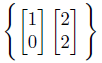
前回の基底が、ちゃんと「一次独立」になっているかを確認します。
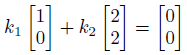
ベクトルのそれぞれに定数をかけて足し合わせます。
これを線形結合と言います。
この線形結合を0にしたとき、定数kはどうなるか?
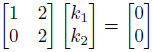
このように変形しても意味は同じです。
kを両方とも0にすれば方程式は必ず成立します。
これを「自明な解」と言います。
自明な解しかもたない場合、「一次独立」です。
でも、そうでない解も存在するかもしれません。
存在した場合、「一次従属」です。
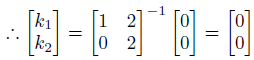
左辺の行列は逆行列を持ちます。
したがって、上のような変形ができ、定数kは一意に0と決まります。
自明な解しか持たないので一次独立であり、この2つのベクトルがあれば2次の数ベクトルの全てを表し尽くせます。
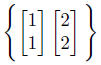
最初のパターンを見てみます。
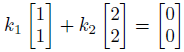
同様に線形結合を見てみます。
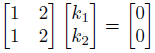
行列で表現をします。
左辺の行列が逆行列を持てば、上と同じ計算で一次独立です。
しかし、この行列の行列式は0で、逆行列を持ちません。
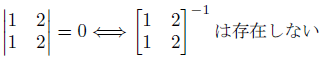
したがって、定数kの解は無数に存在します。
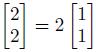
たとえば、さっきのような関係があります。
だから、このベクトルは一次従属で、2次の数ベクトルの全てを表し尽くすことはできません。
「基底」の定義をあやふやにしてきました。
が、一次従属なベクトルがあるということは、正確には基底ではありません。
正確な基底の定義は過不足があってはいけないのでした。
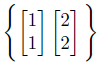
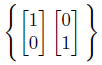

コメント