9/26の応用数学の授業より、フーリエ級数の係数の求め方の話です。
そもそもフーリエ級数ってなんだって話ですが、細かいことは省略。
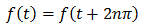
扱うのは、このような周期関数です。
周期2πごとに全く同じ波形が繰り返される関数を扱います。
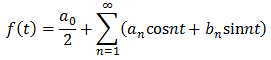
同じ関数をこのように、展開することができます。
つまり、ある周期関数を三角関数の和として表すことができるのです。
ここで、aとかbとかいう三角関数の重み付けの係数が出てきます。
これをどうやって求めるかというのが今回の話です。
ここで、表題の直交関数系の話に移ります。
直交関数系とは・・・
集合{Φk}における2つの関数が
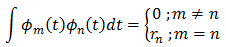
のとき、区間a
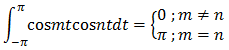
であり、確かに余弦関数は、-π
三角関数と周期関数の積を-π
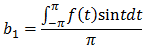
「m=nでないときは全て0」になり消えてしまうので、m=nの項だけが残るのです。
こうして、一つ一つの項を抽出することができます。
これを一般化すると以下の式が得られます。
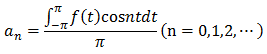
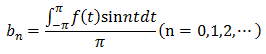
直交関数系というやつは、必要な項以外を見事に消してくれる優れものなのでした。
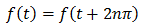


コメント