問題は、いかにタイムを予想するかです。
最初の壁は、コースによって当然タイムが全然違うこと。
そして、いつも同じコースを走るとは限らないこと。
それぞれのコースに対してモデルを作るのは、面倒だしデータ数が少なくなりがちです。
そこで、すべてのコースを「ある理論上のコースに置き換える」という方法を使います。
ここでコースと言っているものは、3つの要素の組み合わせです。
まず競馬場が、札幌から小倉までの10ヶ所。
そして距離が、1000mから3600mまで。
あと、芝かダートか障害かというのがあります。
こういうと「組み合わせは何万通り」みたいな感じですが、実際にはそんなにないです。
障害はもともとデータ数が少なくてアテにならないので除外します。
その中で1年に10回未満しか使われないコースも除外すると、75種類に絞られます。
この75種類のコースで1年のレースの93%を占めています。
コースをいくつか削ったからと言って、賭けるチャンスが極端に減るわけではありません。
ここで注意点。
障害を除くことと10回という数字に、統計学的な根拠はありません。
ここは後で再考することになるかも。
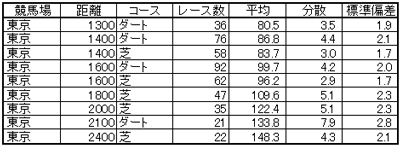
2008年の東京競馬場のコースに対する、平均と分散と標準偏差を示します。
当然、すべての競馬場に対して計算します。
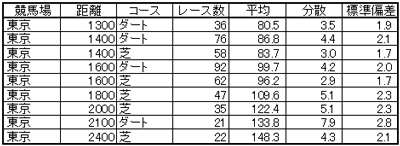
「ある理論上のコースに置き換える」という作業をします。
理論上のコースとは、「平均が0、標準偏差が1」のコースです。
置き換えるというのは、「コースの平均と標準偏差を使った一次変換」です。、
どのコースで走った場合のタイムも、このコース上のタイムに置き換えられます。
全てのデータに対して、それぞれ一次変換を施します。
すると、全部のデータが同じコースを走ったように見えます。
ここでも注意が必要です。
この方法で「芝1000mを走った結果」と「ダート3600mを走った結果」を比較できます。
でも、これは距離とか芝とかの特性を完全に無視してます。
これも再考の余地ありですね。
結果が現実に合わなければ、また戻ってくるとして。
とりあえずは、この方針で行きます。
ところで、この方法は「標準化」と言います。
実は身近なところで使っていて「偏差値」もこの方法です。
国語の点数と数学の点数は直接は比較できませんが、偏差値にすれば比較できます。
これと一緒の原理です。

コメント