ノートの第一回の話題に選んだのは、ボード線図です。
板か何かのboardだと思っていたら、Bodeさんという人名だったようで。
つまり、人名がつくほど偉大な発明だったようです。
こんな単純な図の一体何が。
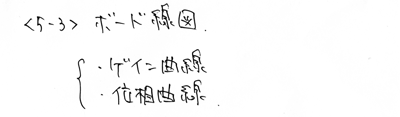
ボード線図の構成要素は、ゲイン曲線と位相曲線です。
複素数の絶対値と位相を周波数軸に対して、別々に書いたようなものです。
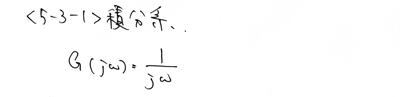
例を示します。
この関数が、なぜ積分系なのかは疑わないでください。
ラプラス変換のあれです。
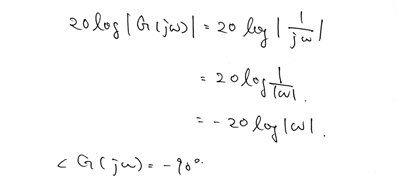
絶対値と位相を計算します。
絶対値に関しては対数をとるところがボード線図のポイントです。
計算はどうでも良し。
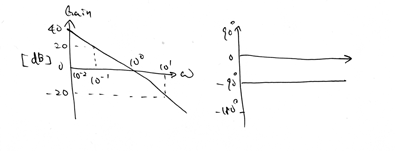
グラフに書き表すとこんな感じになります。
この二つをセットにしてボード線図といいます。
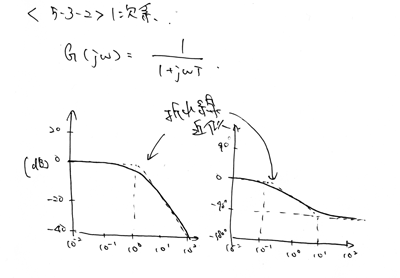
1次系というこの関数についても同様にボード線図が書けます。

2つの図をセットにしているのは、ゲインが同じでも位相が違う場合があるからです。
この二つの関数の場合を例に挙げます。
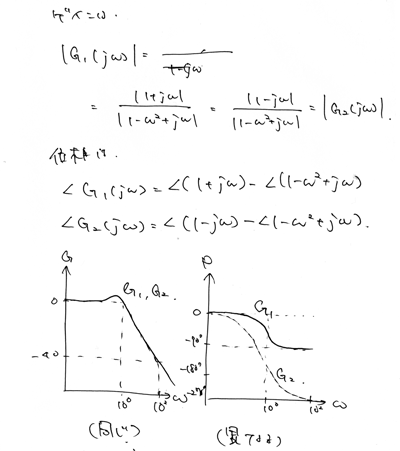
ゲインは同じですが、位相が異なります。
つまり、別の特性を持つ関数であるということです。
なぜ、ボードさんの名前がつくほど偉大な発明だったのか。
それを考えていきます。
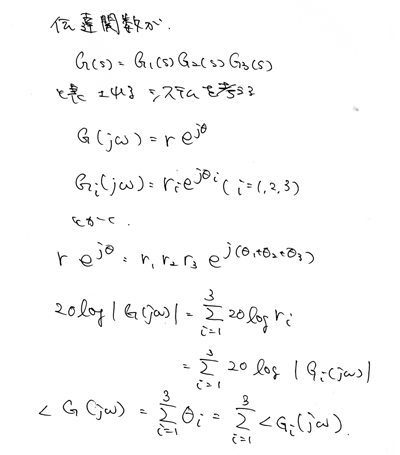
関数がいくつかの関数に分解される場合を考えます。
分解の仕方については後で書きます。
計算式はどうでも良くて、ポイントは最後がシグマになっていること。
つまり、和になっていることです。
ゲインについては対数をとりましたが、これは積を和にするためだったのです。
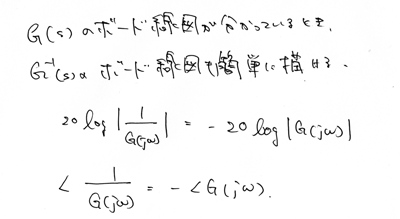
更に、逆関数のボード線図も簡単に書けます。
これも対数のおかげ。
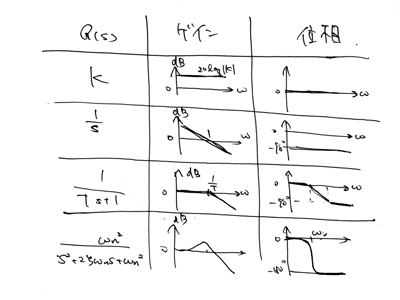
この4つの関数のボード線図が描ければ、後は単純なグラフの足し算で済みます。
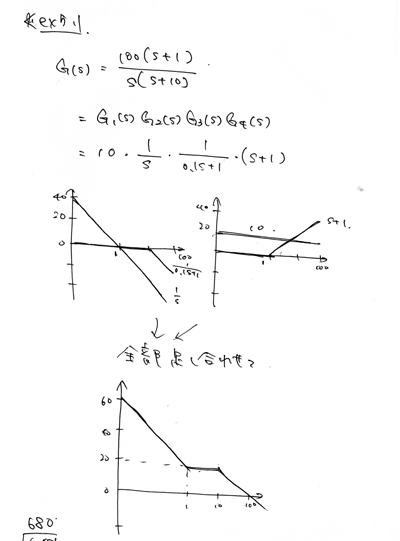
これは一例。
4つの関数に分割して、ここではゲインだけですが、それぞれのボード線図を書きます。
そして、それを足し合わせるだけで複雑な関数のボード線図も描けます。
グラフを対数にしただけで、こんな簡単になるということ。
これがボード線図の凄いところです。


コメント