電気回路

色々とやらなきゃいけないことはあるけど、受験勉強を開始しました。
まずは電気回路。

といっても、キルヒホッフの法則とか素子特性とかは省略。
復習するまでもないです。

使うのは、この本。
2年生の前期に使っていた教科書です。

要するに電気回路を解析するというのは、微分方程式を解くことです。
そして、微分方程式は数学やら力学でも使うので、しっかり学ぶ必要がある。
というわけで、最初にやることにしたのでした。

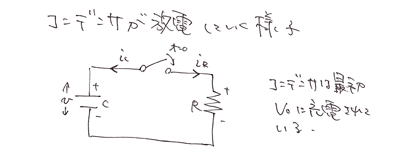
たとえば、こんな回路。
充電されたコンデンサに抵抗を接続したときの、コンデンサの電圧の変化を求めるものです。

微分方程式はこのように書けます。
この導出までは電気系の人なら、まずできるはず。

この形は1階微分方程式と言います。
ついでに、初期値も指定しておきます。

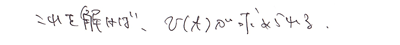
ですよね。

1階微分方程式の余解はこの形になります。
あとは、この中の定数kとsを求めれば良いです。

sは、この式を微分方程式に代入することによって。
kは、初期値を代入することによって求められます。

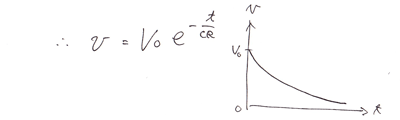
得られた結論はこれ。
指数関数的に電荷が放電されていく様子です。