RCの場合と、RLの場合は、回路方程式は1階微分方程式になります。
でも、1階微分方程式では、LCが同時に含まれる回路は解析できません。
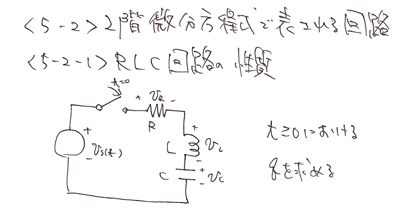
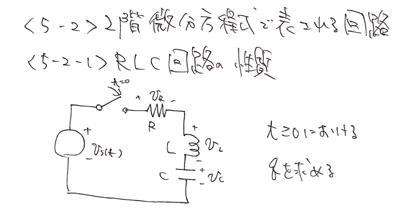
続いて直列RLC回路の解析法を考えてみます。
これは、qの2階微分方程式として表わせます。
2階微分方程式になっても、1階の時と同じような方針で解けます。
つまり、余関数と特解にわけて、それぞれを求めるわけです。
が、少し複雑になることもあります。
たとえば、特性方程式が2次方程式になります。
ので、特性根が2つになり、以下の3つの場合に分かれます。
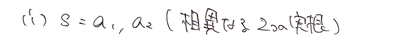
まずは、特性方程式の判別式が正のパターンです。
つまり、根が実数で異なる場合。
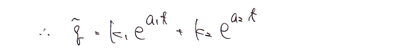
これは、最も簡単なパターンで、1階微分方程式の拡張で単純な良いです。

続いて判別式が0のパターン。
つまり、重根の場合。
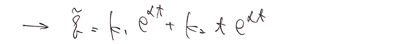
これは少し考察してやると、こんな感じになります。
指数関数にtをかけた成分を追加するわけですね。

最後は判別式が負の場合、つまり複素共役解の場合です。
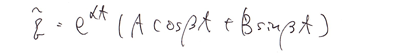
これも少し考察すると、こんな余関数が得られます。
この3パターンのいずれかが余関数になります。
そして、もうひとつ、特解を求めなければなりません。
これは、1階微分方程式の拡張で良いです。
少しイレギュラーな場合もありますが、大抵は大丈夫です。
これで、フェーザを使わない電気回路は大丈夫・・・かな?


コメント