最近、頭が煮詰まってきました。
少し落ち着く必要があるかも。
統計学を使って競馬を予想しようという試みでした。
資金の運用法については、「ケリー基準」という一つの答えに辿りつきました。
この方法が正しい方法かについては、学者さんの間でも未だに議論されています。
その内容を読んだ限り「問題はない」と判断して、これを使うことにしました。
そして、統計学の勉強を始めてみると、競馬は「多変量データ」を扱う問題だということが分かりました。
1つの「ケース」に対して、複数の「データ」があるということです。
競馬でいえば、1つの「出走」に対して、「騎手」「馬場状態」「前走のタイム」などの複数の「データ」があります。
これを扱うのが「多変量解析」というやつで、さらにこれを勉強することに。
テキストを追加しました。
ひょっとするとExcelや自分で書くプログラムでは追い付かずに、統計ソフトの勉強もしなければならないかも。
「ケリー基準」を使うためには、競走馬の勝率を知る必要があります。
これを統計学で求めるわけですが、勝率の前に「タイム」という変数をかませることにしました。
この方が統計学が使いやすいと思ったからです。
そして、多変量解析の中の「重回帰分析」という手法でタイムを予想できそうだということが判明。
目的変数が、タイム。
説明変数が、前走のタイムや騎手などの色々なデータです。
これが複雑にからみあっているせいで、頭の中がぐちゃぐちゃになっています。
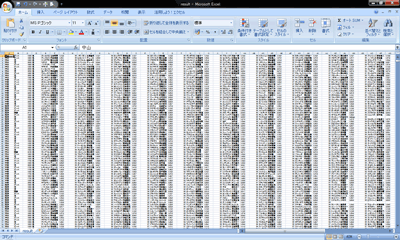
取得してきたデータがこんな感じ。
やっと20万件分くらい整理できそうだけれど、全部で100万件くらい扱うつもりです。
この100万というのは、縦の数で、つまり行の数で、これが多いほどデータは正確になることでしょう。
だから、これは多ければ多いほどいいです。
処理に時間がかかる以外は、その方が嬉しいです。
問題は、横の数、つまり列の数です。
これは、重回帰分析のところでも述べたように、お互いに影響しあいます。
で、その影響は取り除いてやらないといけないです。
そして、列の数が増えるほど、影響の及ぼし合い方は複雑になり、手に負えなくなります。
すでに僕の手には負えなくなっています。
可能な限り、理論的に攻めたいんだけど、「理論的に」と思いすぎると進めなくなる。
ある程度は「工学的に」攻めないといけないんだろうけど、どこまで妥協が許されるかが分からないから難しい。
「標準化」という方法も述べたけれど、あれも実は勘違いをしていて厳密には使えやしないことに気付きました。
さらに、重回帰分析はタイムをピタリと出しやがるから、これも問題です。
欲しいのは、正確にはタイムでなく、タイムの確率分布なんですよ!
いかにも日記らしい日記が書けたぜ!
でも、こんなことを書きながらも、大事な発見をしたので良し。

コメント