重回帰分析

説明変数が1つの時は回帰分析でした。

でも、このように説明変数が2つ以上ある場合は重回帰分析を使います。
どちらも二乗誤差を最小にするという方法で求めます。
最小二乗法ですね。

説明変数が2つになると何がやっかいかと言えば、説明変数同士が依存しあってしまうことです。
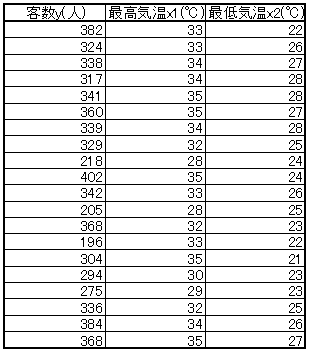
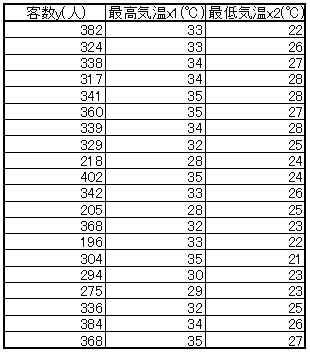
最高気温と最低気温を説明変数にしようとした場合を考えます。
最高気温が高い日の最低気温は比較的高くなる傾向があります。

この影響を取り除きながら、重回帰式を作らなきゃならないわけです。

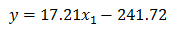
これは最高気温だけを利用した回帰直線です。
説明変数が1つだから、平面上の直線でした。

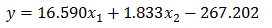
最低気温を含めると説明変数が2つになるから、今度は空間中の平面になります。
面はExcelじゃ描けないので、使い慣れないMaximaを使ってみます。

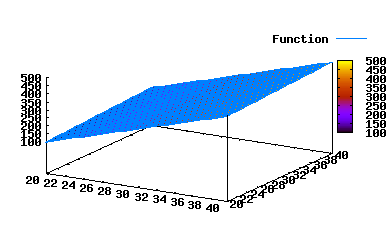
こんなもんですね。
重回帰が使えれば、かなり分析の範囲は広くなります。
でも、まだ条件が残っていて、これらは量的データにしか使えないのでした。

アイスクリーム屋さんの客数に影響を与える要因として、天気も考えられます。
天気は「晴れ」とか「雨」とかです。
これは数式に入れられないので、回帰分析ができません。

この「晴れ」とか「雨」とかを、なんとか数値化してやりたい。
このため方法を数量化法といいます。
･･･が、この方法は理解してないです。
難しいよ。