ケリー基準(3)

半分ケリーと1.5倍ケリーは数学的に同じだと書きました。
･･･が、嘘でした。

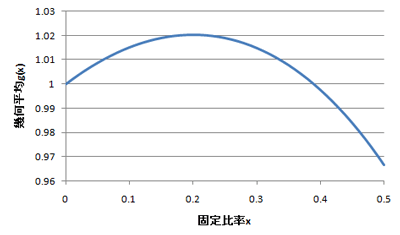
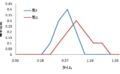
このグラフが、x=0.2を中心にして対象かと思っていたけど、そんなことないです。

半分ケリーの幾何平均は、1.0152です。
1.5倍ケリーの幾何平均は、1.0149です。
ほとんど同じだけど、少し違いましたね。

ちなみに、2倍ケリーの幾何平均は、0.9976です。
つまり、ケリー基準の2倍の比率で賭けていくと、どんどん損をします。
利益の期待値がプラスのゲームなのに･･･ですよ！

正確な期待値が計算できれば、ケリー基準で賭けていくのが正解です。
でも、実際に計算した期待値には誤差が生じるでしょう。

この誤差によって賭ける比率が大きくなってしまったり小さくなってしまったりします。
このとき、小さくなった場合はまだラッキーですが、大きくなった場合はアンラッキーです。
幾何平均が微妙に違うとか、そういう問題ではありません。

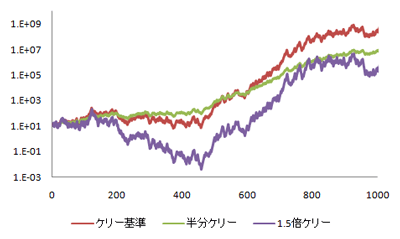
この通り、賭ける比率が大きくなるほど、グラフが乱高下するんです。
半分ケリーの落ち着きに対して、1.5倍ケリーの上下のひどさですよ！

グラフが乱高下するのは、精神的に良くないです。
このグラフでも、限りなく破産に近いところまで行ってますし。

乱高下してるくせに、長期的にみると利益はほぼ一緒なんですよ！

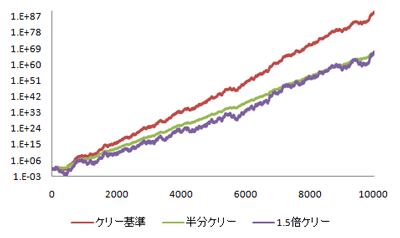
だったら、グラフが落ち付いている方が良いでしょう。
しかも、上で述べたように、ケリー基準を大きく突破して約2倍を超えると利益はマイナスになります。
逆に小さすぎても絶対にマイナスになることはありません。

というわけで、ケリー基準を越えた比率を賭けるくらいなら、控え目に賭けた方が良い。

以上の考察から作戦はこうなります。
過去の競馬のデータから期待値とその誤差を計算する。
誤差の範囲を考えてもケリー基準を越えないように比率を決める。

あとは、そのための期待値と誤差を統計学を使って導き出すだけかな。
でも、ケリー基準もまだ終わりません。