相関係数

回帰分析をする上で欠かせない指標が「相関係数」です。
良く考えたら、最初にこれを書くべきだった。

相関係数の定義は複数ありますが、これは「ピアソンの積率相関係数」という定義。
共分散を標準偏差で割ったものです。

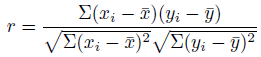
統計指標は、数式で書くと複雑になりがち。

標準偏差は分散の平方根なので、共分散を分散で割ったものと思っても良いです。
共分散自体が相関らしきものを表しています。
が、そのままでは相関の大小を評価できないので、分散で規格化するわけです。

規格化された相関係数は、-1から1の値をとります。
絶対値が相関の強さ。
正負は相関の正負を表します。

実際に目で見た方が早い。

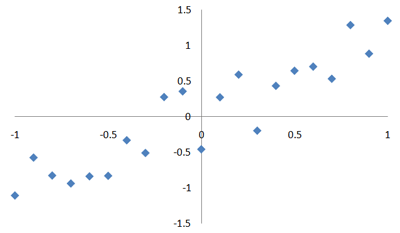
相関係数、0.92。

絶対値が大きいので、しっかりと右上がりの傾向が出ています。
「右上がりの傾向」は「正の相関」と言います。
正の相関だから、相関係数の値も正です。

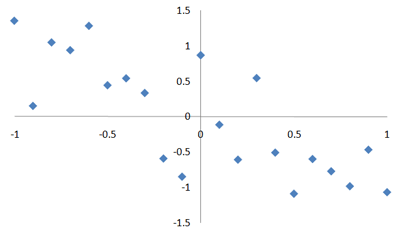
相関係数、-0.79。

さっきよりも絶対値が小さくなりました。
それにしたがって、プロットがばらついたように見えます。

相関係数は負で、「負の相関」です。
「右下がり」です。

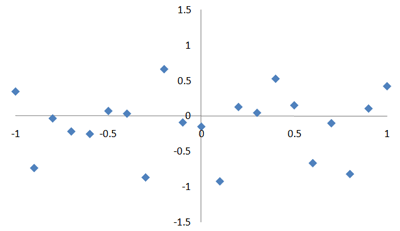
相関係数、0.06。

絶対値がきわめて小さい場合。
もはや傾向は見えません。
バラバラです。

相関係数は正ですが、値が小さいので、「右上がり」には見えません。

回帰分析をするときは、相関係数がある程度の大きさを持っている必要があります。
やみくもに回帰分析をしても、そこに相関がなければ意味がありません。