解くべき方程式は、こちら。
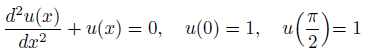
次に近似式を用意します。
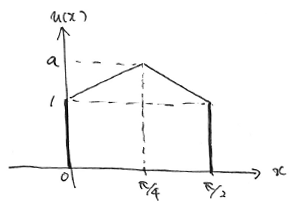
今回は領域を2つの要素に分割して近似します。
要素を2つにするということは、節点が3つになるということです。
そのうちの2つ、左右の値は境界条件によって与えられています。
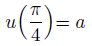
中間の値を定数aとおきます。
微分方程式の解の誤差ともいうべき「残差」が小さくなるように、定数aの値を定めるのが目標です。
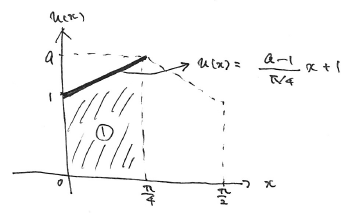
左の要素での直線を式で表現してみます。
一次方程式なので中学生でもできます。
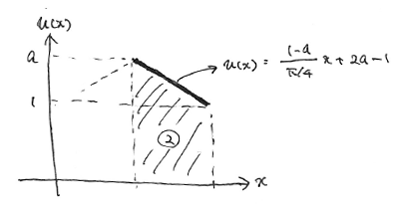
右半分も同様。
これで近似解が得られました。
厳密解は三角関数でしたが、ここでは要素で分割された1次関数と近似しています。
重み付け残差法に必要なものは、「近似解」と「重み関数」でした。
というわけで、次は重み関数を考えて、実際に微分方程式の解を求めてみます。
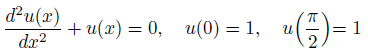
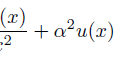
コメント