ラプラス変換を利用して微分方程式を解いてみます。
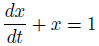
数学では、1つのものを色んな角度から見ることがあります。
ラプラス変換による微分方程式の解法も同様です。
微分方程式を、ずっと微分方程式の世界で解き続ける方法がひとつ。
これは前回までの解法。
微分方程式を一度ラプラス変換の世界に持ち込んで、再び微分方程式の世界に戻ってくるという方法も一つ。
これが今回の解法。
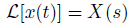
ラプラス変換を大文字で表わします。
独立変数は、tからsになります。
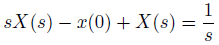
微分方程式の両辺をラプラス変換すると、こうなります。
これで、ラプラス変換の世界に持ち込むことができました。
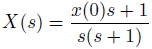
ラプラス変換の世界で、Xを求めます。
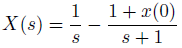
部分分数分解するのは、逆変換するための定石です。
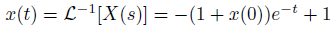
ラプラス逆変換をします。
これで、元の微分方程式の世界に戻ってくることができました。
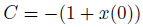
定数を分かりやすくするために定義しなおします。
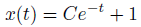
すると、無事に前回と同じ解が得られました。
対象とするものを一番扱いやすい世界で扱うと良い。
そのために、優秀な数学者がいろんな世界を創造してくれているのです。
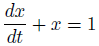
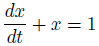

コメント