早速、単回帰分析してみよう。
まずは、大まかに解説。
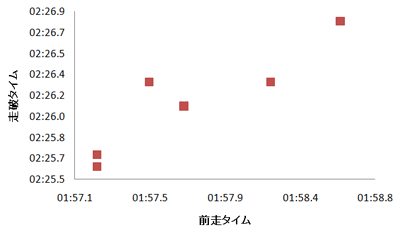
赤色のような沢山のプロットを、一本の線で表現するのが回帰分析です。
「プロットの真ん中あたりを通るような線をフリーハンドで引いてください」
と言われたら、なんとなく書けそうなくらい傾向は出てますね。
回帰分析は、「なんとなく」ではない理論的に誤差の小さい直線を引いてくれます。
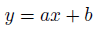
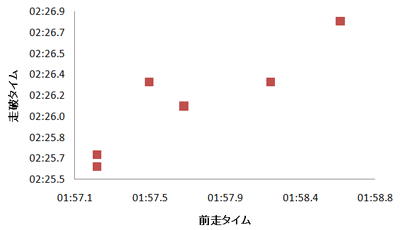
これは直線の式です。
この式を回帰直線の式とみると?
回帰分析とは要するに、このaとbという係数を統計学的に定めるということです。
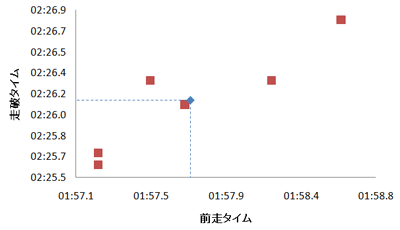
グラフ中の青色は平均です。
平均なんて説明するまでもないかもしれないけれど一応。
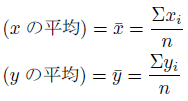
サンプルを全部足し合わせて、サンプル数で割るだけ。
沢山のプロットを表現する直線は、平均を通るのが自然ですよね。
そういうわけで、平均の点を通るという条件で、係数が一つ定まります。
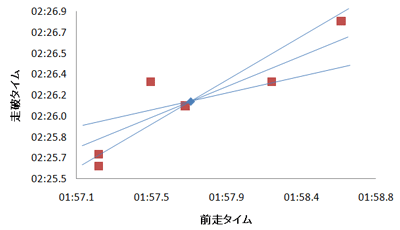
傾きが不定だと、無数の直線が引けてしまう。
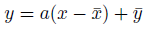
式で言うと、こういう状態。
あとは、この直線の傾きを求めるのみです。
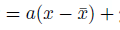
コメント