逆運動学

難しいのは逆運動学です。

リンクが1本しかないとしても、逆三角関数が出てきます。
2本以上になると加法定理を駆使しなきゃならなくなります。

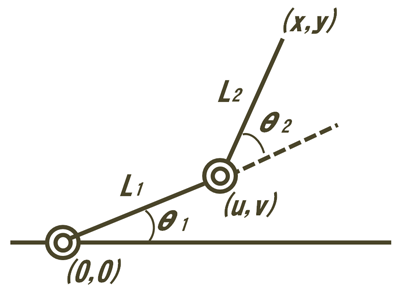
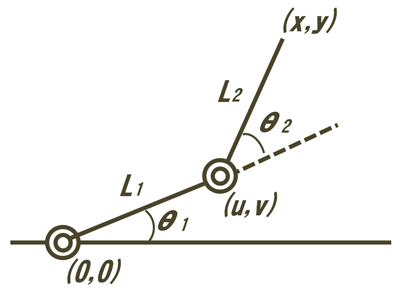
図を思い出します。
(θ1,θ2)を求めるのが逆運動学です。

手先の位置から、直接的に、関節の角度を求めるというのは無理です。
もし、できるなら教えて欲しい。

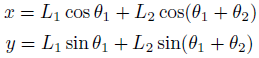
仕方がないので、前回の順運動学の答えを再掲。
これをうまく式変形して、θの式にできればゴールです。
いかにも大変そうです。

いざ、2リンクマニピュレータの逆運動学。
まずは、2つめの関節の角度から求めます。

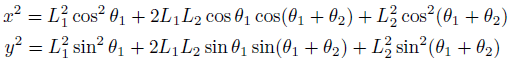
男は黙って両辺を2乗。
三角関数を消去する手段として、三角関数を2乗するという方法があります。

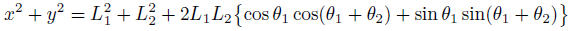
足し合わせると、三角関数の性質より嬉しいことが起きます。
ただ、厄介な項が生じました。

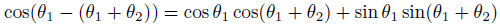
が、恐れることはなくて、加法定理により綺麗にまとまります。
嬉しいのは、θ1の項が消えてなくなるということです。

まとめると。

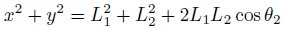
あとは、移項とcosの逆関数で計算終了です。

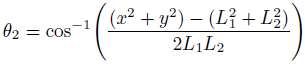
結論は、こちら。
なかなか険しい道ですが、求められます。

が、もう1つの角度を求めるのはかなり辛いです。