移流項と拡散項

マイナーな偏微分方程式を除けば、偏微分方程式はいくつかのパターンに分類されます。
その中でも、移流拡散方程式はイメージがしやすい。

例によって、係数は省略しています。

(1)移流方程式

右辺の位置の1階微分を「移流項」と呼びます。

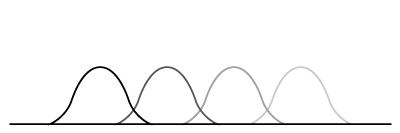
この方程式の解は、時刻tの経過と共に関数がそのままの形で移動するような解になります。
移動して流れる方程式、移流方程式ですから。

(2)拡散方程式

右辺の位置の2階微分を「拡散項」と呼びます。

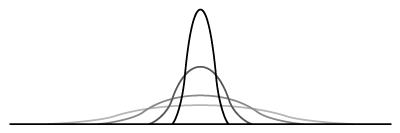
この方程式の解は、時刻tの経過と共に関数が広がっていくような解になります。
これが拡散方程式の「拡散」の所以。

(3)移流拡散方程式

右辺に「移流項」と「拡散項」を含む方程式です。

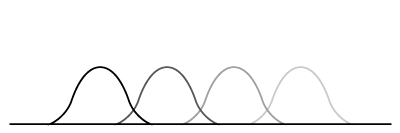
この方程式の解は、時刻tの経過と共に関数が広がりながら移動するような解です。
移流方程式と拡散方程式を自然に組み合わせた解です。