偏差の2乗を最小化します。
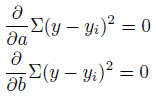
最小化といえば、「微分して0とおく」ですね。
数学屋の人たちに、「ちゃんと増減を調べろよ」と言われそうです。
実際には、これで得られる答えは、「最小値」じゃなくて「極値」です。
が、計算対象の性質から最小値が存在するとわかっている時は、これで良しとします。
計算してみて、解が2つも3つも出てきた場合に初めて「本当に最小値であるか」を確認します。
工学系人間は、こういうところでテキトーです。

ごたごたと計算。
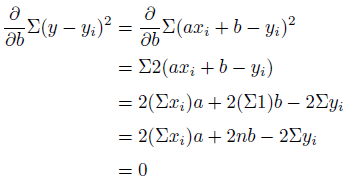
こちらも、ごたごたと計算。
簡単な微分だけなので問題ないでしょう。
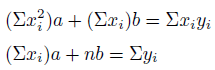
こうして、aとbの連立方程式が得られました。
あとは、これを解くだけ。
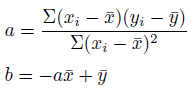
解がこちら。
そして、これを直線の式に代入すれば、回帰直線の出来上がりです。
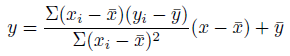
まとめ。
単回帰分析はこんなもん。
説明変数が2つ以上の重回帰分析も手順は同様です。
ただ変数が増えることの複雑さがあります。
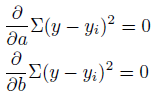
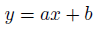

コメント