数学の学習の詰めの作業に入ってます。
大学の教科書に何故か載っていなかった定理。
ケイリーハミルトンの定理。
・・・思い出せますか?
思い出せませんでした。
ので、Wikipediaしました。
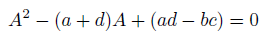
こうだったかー!
Maximaで確かめてみます。

正しい。
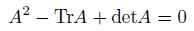
考えてみたら、こうも書けますね。
・・・なんか見覚えのある形。
というわけで、話が脱線します。
2次の正方行列の固有値を求めてみます。
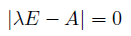
固有方程式とか言いますね。
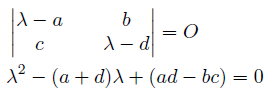
成分にして計算してやると、こんな具合。
・・・で、脱線していた話が元に戻ります。
2次の固有方程式はケイリーハミルトンの定理と同じ形でないか!
λの所に行列Aを入れたら、ケイリーハミルトンの定理そのものではないか。
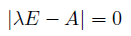
またまたこの式に戻ってみると。
λの所に行列Aを入れたら0になるのは、当たり前です。
つまり、ケイリーハミルトンの定理なんてその程度のものだということです。
大学の教科書に書くほどのものではないと。
同じ発想で、ケイリーハミルトンの定理の3次バージョンも簡単に作れます。
3次行列の固有方程式を作って、λの所にAを代入するだけです。
復習はじっくり。
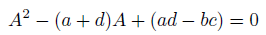

コメント