こんにちわ。
amazonでIllustratorを注文したら、実はMacintosh版でした。
へこんでます。
キャンセル不可とな・・・。
気を取り直して、今日も元気に回帰分析していこう。
回帰直線の傾きは、共分散と分散の比で得られました。
その数学的根拠を説明していきます。
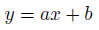
回帰直線。
回帰係数aとbを統計学的が決まっていれば、xからyを予測する式になります。
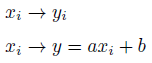
第1式、説明変数は目的変数と対応します。
第2式、目的変数がまだ分からない時は予測式を用いて予測するしかありません。
上の式は過去のデータで、下の式は未来を予測するデータです。
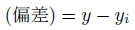
予測と現実の差を「偏差」と言います。
この偏差は、予測の誤差ともいえるので、小さい方が良いです。
この偏差を最小にするのが回帰分析です。
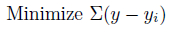
「偏差を最小化する」というのはシンプルですが、これはダメです。
偏差はマイナスになりうるのが、その原因です。
「y=-∞」が解になりますけど、当然、意味はありません。
「偏差の和をゼロにする」なら、まだマシです。
が、誤差が誤差を相殺するので、やはり意味はない。
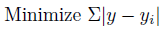
そこで、偏差が負の値を持たないようにする。
つまり、「偏差の絶対値を最小化する」という方法が考えられます。
これなら、数学的根拠となります。
だけど、回帰分析でこれを使わないのは、絶対値の扱いの問題にあります。
絶対値は、正負による場合分けが必要になるのが、主な問題。
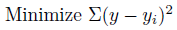
そこで「偏差の2乗を最小化する」というのが、最適なようです。
つまり、「最小二乗法」です。
二乗誤差の最小化といえば、他にも色々な近似に使われています。
フーリエ級数が周期関数の最良近似である根拠も、二乗誤差の最小化にあります。
次は、実際に偏差の2乗を最小化する計算です。
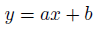
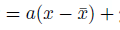
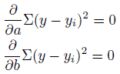
コメント