回帰分析(2)

久しぶり記事。
春に熱中した多変量解析について書いていきます。

「競馬のために勉強した」というと動機が不純ですが、非常に便利なので。
もちろん他の多くの分野にも適用できます。
ひょっとしたら卒業研究にも使うかもしれないので、ここらで復習。

多変量解析は、その名の通り、多くの変量、つまり変数を扱う解析法の総称です。
具体的には、主成分分析、因子分析、クラスター分析などです。

その中で、一番便利だと思うのが、重回帰分析です。

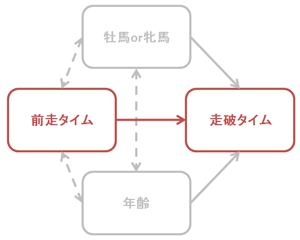
競馬をネタにすると学問的に残念な感じですが、考えやすいので。
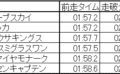
赤色に注目。

次のレースを走る馬がどのくらいのタイムで走るかが分かれば、大儲けできますよね。
これを予測する理論が「回帰分析」です。

予測したいもの、この場合は「走破タイム」のことを、「目的変数」といいます。
目的とする変数だから、目的変数。

そして、「走破タイム」を予測するためのヒントになるものを探します。
たとえば、「前走のタイム」が早い馬は、次の「走破タイム」も早いだろうと考えて、これを利用することにします。

予測のヒントになるもの、「前走のタイム」のような変数を「説明変数」といいます。
目的変数を説明するための変数だから、説明変数。

単回帰分析は比較的シンプル。
Excelの機能で簡単に計算できます。

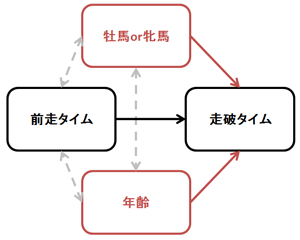
さっきはヒントが1つでしたが、ヒントは多い方が良いと考えます。
そこで、「牝馬or牡馬」と「年齢」をヒントに追加します。
ちなみに、牝馬(ひんば)っていうのはメスの馬で、牡馬(ぼば)っていうのはオスの馬です。

説明変数が1つの時を「単回帰分析」、2つ以上の時を「重回帰分析」と言います。

単回帰分析はシンプルですが、重回帰分析は複雑です。

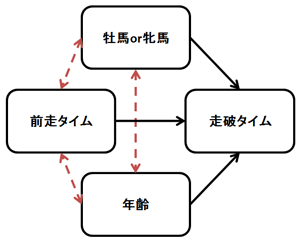
重回帰分析が複雑な理由はというと。
目的変数が複数になるので、「目的変数同士の相関」を考える必要があるからです。

更に、何を目的変数とするかも考える必要が出てきます。
一見、説明変数に影響を及ぼしている目的変数が、実は意味のない変数だったりします。
しかも、そういう変数を含めてしまうと、間違った結果を導いてしまいます。

そういうわけで、重回帰分析は確かに複雑。
でも、線形な回帰分析なので、割とシンプルに計算できます。
線形代数フル活用で。