研究室合宿で、一瞬だけ話題になり、既に忘れ去られた問題。
12枚の硬貨がある。
そのうち1枚だけが偽装硬貨で、本物とは重さが異なる。
天秤を3回使って、偽装硬貨を特定せよ。
ポイント。
・偽装硬貨は、本物より重いかもしれないし軽いかもしれない。
・天秤は重いか軽いかの情報しか得られない。
「偽装硬貨は重い」とかってヒントがあれば随分簡単なものです。
でも、それが分からないと物凄い難問。
本当に答えがあるのかすら疑わしくなってきます。
で、この問題について、「基礎情報理論」の本に記述がありました。
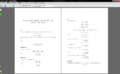
12個のうちのどれが偽装硬貨なのか、偽装硬貨は重いのか軽いのか。
その情報量はというと。
つまり、どのくらいの情報量が欲しいかというと。
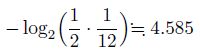
天秤を1回使うことで、重い・軽い・同じのどれかの情報が得られる。
こちらの情報量はというと。
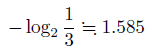
つまり天秤1回で、これだけの情報量が得られるということです。
天秤の情報量3回分で欲しい情報量をこえることができます。
というわけで、天秤を3回使えば、必ず偽装硬貨を特定できるということ。
ついでに、硬貨の枚数と情報量の比較をご覧あれ。
3枚からしか載せていないのは、2枚ではどちらが偽装硬貨か特定しようがないためです。
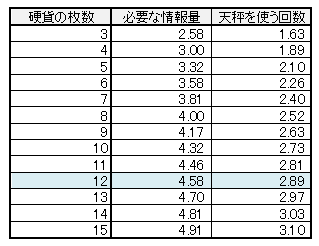
ということは、天秤が3回使えれば、13枚までいけると?
12枚でも難しいのに・・・。
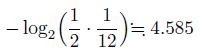
コメント