1次元のヘルムホルツ方程式は厳密解が簡単に求められます。
まず、ヘルムホルツ方程式を紹介。
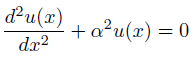
訳の分からない名前がついているから、ひるんでしまいそうだけど。
良く見ると、見覚えのある式です。
位置の微分を時間の微分とみれば、単振動の式と同じです。
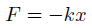
フックの法則より、ばねにかかる力は位置に比例する。
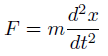
ニュートンの運動方程式。
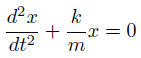
力の項を消去すれば、単振動の式が得られます。
これを逆に利用して考えると。
ヘルムホルツ方程式の解も、単振動と同様に三角関数を含む解になりそうです。
実際に解いてみる前に、定数と境界条件を与えておきます。
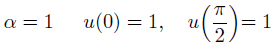
解が簡単になるように設定してあります。
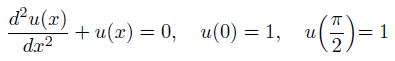
まとめると、これを解くということ。
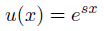
線形微分方程式を解く時の定石ですが、指数関数を代入してみます。
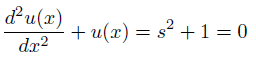
このsの多項式を特性方程式と呼ぶこともあります。
2次方程式なので簡単に解けます。
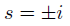
解が2つ出てきたので、基本解が2つ。
その線形結合をとれば一般解です。
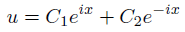
これが一般解。
虚数は落ち着かないので、変形します。
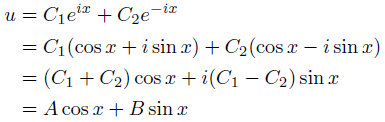
ようやく一般解が完成。
予想通り三角関数になりました。
最後に、境界条件を代入します。
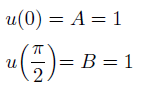
積分定数が得られ、これで特殊解の完成です。
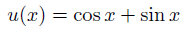
微分方程式の解法を説明するのは長い道のりです・・・。
とりあえず、解が得られました。
次は有限要素法を使って近似解を求めてみます。
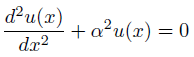
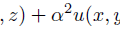
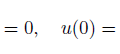
コメント