大数の法則という言葉自体は中学校で習うはずなので、だいたいの日本人は知っているはず。
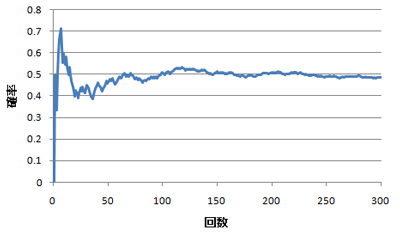
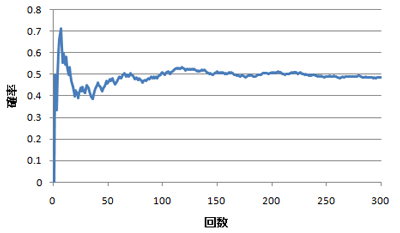
これは、コインで表が出る確率のモンテカルロシミュレーションです。
1回投げた時点で、確率0%と求められました。
10回投げた時点で、確率70%。
50回投げた時点で、確率45%。
300回投げた時点で、確率は49%。
数字より図を見た方が早いけれど、回数をかさねるごとに確率は真の値に近づきます。
これが大数の法則です。
ここまでは中学生の教科書にも載るように、直観的に分かります。
・・・で、なんで回数を増やすと正確になるのか?
母集団と標本の考え方を、引っぱり出します。
この実験での、母集団というのは、無限回コインを投げた結果です。
標本は、10回とか、300回とかコインを投げた結果です。
当然、これらの結果の平均は一致しません。
母平均は50%ですが、標本平均は上のように回数によってフラフラしています。
ただし、標本平均の平均は母平均でした。
10回投げた標本でも、300回投げた標本でも、その確率の平均を取れば母集団の50%に一致します。
そういうわけで、確率の平均というのは、いつでも一緒。
回数を重ねたからといって正確になるものではないです。
回数を増やすと、何が正確になるかといえば、分散です。
コインを投げれば投げるほど、分散が小さくなります。
だから、母平均から極端に離れた値を取りにくくなります。
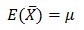

コメント