線形変換

正規直交基底が便利だと分かったので、今回は正規直交基底を前提にします。

ここまでの話で、「りんご2個とみかん3個」というのをベクトルで表現できました。
たった2つの数字を並べるだけで、日本語でいうところの「りんご2個とみかん3個」を表現できたわけです。

このベクトルは基底の取り方を変えてしまったら変わります。
だから、同じベクトルでも表わしている意味が違う場合もあります。

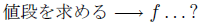
今回は、「値段を求める」という操作を線形代数で表現したいと思います。

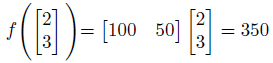
りんごとみかんの数のベクトルに、値段のベクトルを掛け合わせれば良いです。
これだけで値段が求められます。

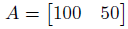
値段のベクトルをAと表現します。
これを線形代数の言葉で「表現行列」と言います。
今回はたまたまベクトルですが、一般には行列です。

「値段を求める」という操作も、たった2つの数字を並べるだけでできるんです。

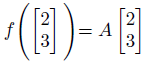
そして、そのような変換を「線形変換」と言います。
なんと、線形性をもつ変換は、必ず行列で表現できるんです。

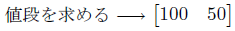
まとめると、こういうこと。
日本語で書くと、「100円のりんご2個と50円のみかん3個の値段を求める」ということなのだけど。
その数字の部分だけを取り出して話ができるってことです。