ここまでで3パターンのベクトルの組み合わせが出ました。
その中で1つは一次従属で、基底でないことが分かりました。
2つある基底のうち、どちらが扱いやすいのか?
実際には基底というのは無数にとれるので、一番良い基底とはどんなものか?
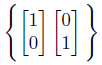
まず1つ目。
この基底を用いて、りんご2個とみかん3個を座標平面に表現します。
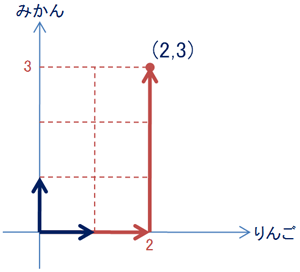
基底となる二つのベクトルを青い矢印で示します。
そのベクトルを定数倍して、足し合わせると、(2,3)の座標に辿りつきます。
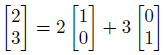
この(2,3)という座標は、前に示したこの式の定数に他なりません。
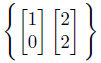
続いて、こちらの基底を用いた場合はどうなるか。
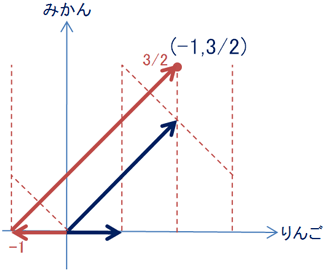
基底の一つが変な方向に向きます。
1つ目のベクトルを-1倍、2つ目のベクトルを3/2倍すれば、前と同じ位置に辿りつきます。
ただ、基準が違うので、座標は(-1,3/2)です。
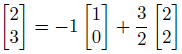
この座標も先ほどと同様に、前に示した式の定数に他なりません。
グラフを見たら、どちらを基底にとるべきかは容易に分かると思います。
前者の方がシンプルです。
なぜシンプルかといえば、この基底が正規直交基底だからです。
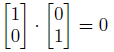
直交基底とは、基底を構成するベクトルがお互いに直交しているということ。
1つ目のグラフでは、青矢印が直交してます。
2つ目のグラフでは、青矢印がおかしな角度になっています。
だから、前者は直交基底で、後者は直交基底ではありません。
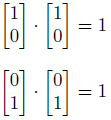
正規基底とは、基底を構成するベクトルの大きさが1であるということです。
1つ目のグラフでは、青矢印は共に同じ長さで1です。
2つ目のグラフでは、矢印の長さが違います。
前者は正規基底で、後者は正規基底ではありません。
前者は、直交基底かつ正規基底で、つまり正規直交基底です。
というわけで、前者を使った方が賢いでしょう。
ちなみに、正規直交基底という条件をつけても、基底は無数に存在します。

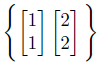
コメント