一般相対論について色々と勉強して、「・・・で結局、どうやって使うの?」というところに辿り着きました。
一般相対論の基本方程式を順番に書いていきます。
スタートは物質の分布です。
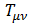
アインシュタインの重力場の方程式と、一般相対論的な運動方程式の連立方程式を解きます。
これらの連立方程式を解くことで、計量テンソルを求めます。
アインシュタインの重力場の方程式です。
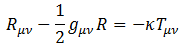
ここで、リーマン・クリストッフェルの曲率テンソルというものが現れます。
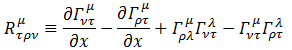
このテンソルのμとνを縮約したものを、リッチのテンソルと呼びます。
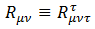
リッチのテンソルから更に派生して、以下のRをスカラー曲率と呼びます。
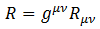
一方、右辺の比例定数κは万有引力定数と光速度を用いて表されます。
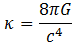
次に一般相対論的な運動方程式です。
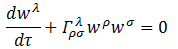
ここで、wは4元速度です。
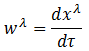
結局、その連立方程式を解くことで、計量テンソルを求めることができます。
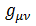
計量テンソルと不変距離dsの式から重力場のある時空の構造が決定されます。
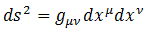
この手順を踏まえて、シュヴァルツシルトの解を求めたりとかできます。
シュヴァルツシルトの解ってなんだって話は、また・・・!

コメント