「平方数と平方数を並べた数で平方数になるもの」を探してみます。
整数 i は、i = 1,2,3,… とします。
整数 j を、j = 1,2,3,…,i とします。
それらの2乗を並べた数が平方数であるか、を調べます。
小さい数字から、たとえば、
49 (4と9)
169 (16と9)
361 (36と1)
1225 (1と225)
1444 (144と4)
など。
まず、このような数字は無限にあるのかという疑問。
平方数と、10の偶数乗の組み合わせは、必ず平方数になります。
よって、無限に存在します。
たとえば、
4900 (49と100)
490000 (49と10000)
49000000 (49と1000000)
など。
無限に存在することが分かったところで、どのくらい出現するのかを考えます。
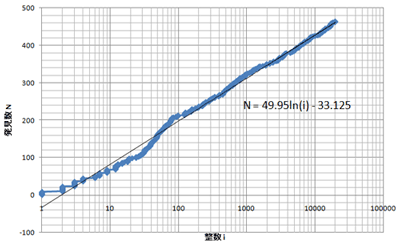
…と、どうやらおよそ対数関数的になりました。
i=1,2,3,…,20000
として、リストアップします。
全部で464個ありました。
整数 i まで調べた時点までに発見した数を N 個とします。
下のグラフのような頻度で出現しました。
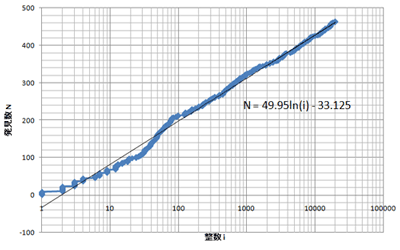
i が大きくなるほど近似曲線との誤差が小さくなってきます。
これからも分かるように、やっぱりこのような数は無限にあります。

コメント