運動学の専門家ではないので、自分なりに答えを導いています。
ので、もっと良い解法があったら教えて欲しいところです。
結構頑張って求めました。
まず、順運動学の答えを再び。
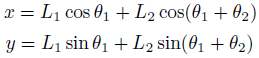
座標(x,y)が与えられたときに、θが欲しい。
前回で、θ2は求められたので、それも利用できます。
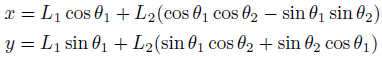
まず、三角関数の中に和が含まれていると扱いにくいので、形を変えます。
加法定理を使って分解しました。
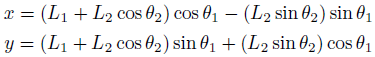
並べ替えただけ。
こうすると、もうθ1の連立方程式になるので、後はゴリ押しで解けます。
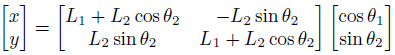
個人的に行列にした方が解きやすいので、そうしました。
運動学は、その線形性のために行列を活用することが多いです。
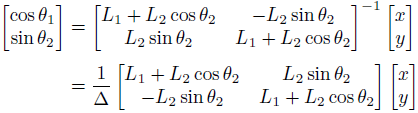
逆行列をかけます。
あとで消えてなくなるので、行列式Δは敢えて計算しません。
実は、この形までくれば、計算はできます。
ある意味ではゴールです。
でも、θ2を含まない形ににしたいので、もう少し頑張ります。
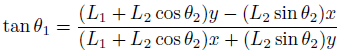
なぜ行列式が消えてなくなるかといえば、比を取るためです。
sinとcosの比、つまりtanを計算しています。
そのまま、cosやsinの逆関数を取れば良いような気もします。
でも、tanにするのが流儀のようだし、その方が綺麗にまとまります。
これの逆関数を取れば良いんだけど、いくら何でも汚すぎる。
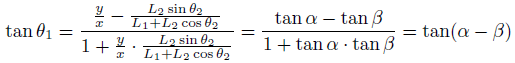
実は、このtanも加法定理で分解できます。
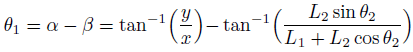
結局、こんな形になりました。
複雑ではあるけど、まあまあ読める形。
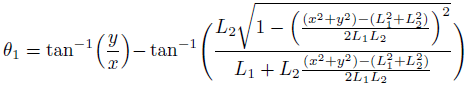
θ2の三角関数については既に求めたので、それを代入しました。
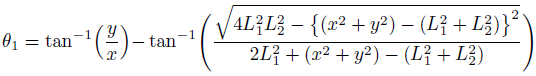
少し整理して、逆運動学の完成です。
リンクが3つになったら、どうなってしまうんだろうか。
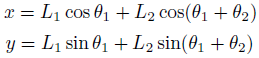


コメント