微分方程式の続きです。
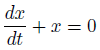
前回はこれを解きました。
特殊解をひとつ求めて、それの任意定数倍が一般解としました。
その根拠は線形性にあります。
まず復習。
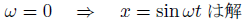
三角関数を解にするようにωを設定しました。
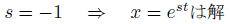
指数関数も解になるようにsを設定しました。
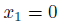
ωを実際に代入してみると、0が解になります。
いわゆる自明な解です。
三角関数は影も形もなくなってしまいましたが・・・。
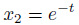
sを実際に代入してみると、指数関数が解になります。
こちらは自明でない解です。
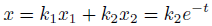
線形性より、解の定数倍や解の和は、やはり解になります。
したがって、これも解。
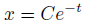
そういうわけで、こうなったのでした。
1階線形微分方程式の場合、任意定数が1つ含まれていれば、全ての解を尽くしています。
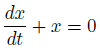

コメント