たまには数学の話をします。
実は院試の勉強の6割が数学に割かれています。
数学おもしれー。
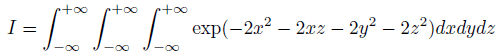
この積分がテーマです。
でも、解くことが目的ではなく、積分変数の変換をいかにしてするかという話。
被積分関数がやや複雑なので、とある変数変換をします。
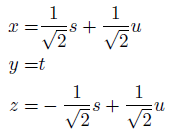
結論だけ出してしまいますが、この変数変換をします。
先の被積分関数を行列の2次形式にして、対角化して、標準形に持ち込めば、この変換をすることになります。
この方法を学んでしまったら、行列から離れられなくなります。
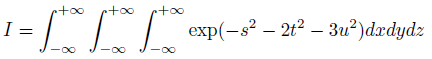
すると被積分関数がいくらかシンプルになります。
この関数はガウス関数なので、さくっと計算できます。
が、積分変数が変換されていないので、積分が実行できません。
「dx dy dz」のままだから、積分できないんです。
これを何とか「ds dt du」にしたい。
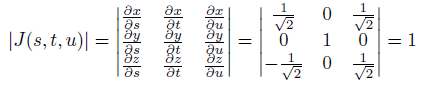
これについて散々悩んで、友人に聞いてみて、弟にも質問してみたところで、自己解決。
ヤコビ行列式を使えば良いのでした。
そういえば、こんなの大学1年生の頃に習ったような気がする。

こういう書き方をすると数学屋さんに怒られそうですが、そこは大きな心で。
要するに、ヤコビ行列式をかけた上で、積分変数を入れ替えれるわけです。
ヤコビ先生、ありがとう!
今回の場合は、ヤコビ行列式が1なので、次のようになります。
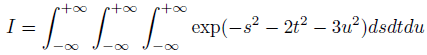
これで積分が実行できます。
ここからは、ガウス先生に頭を下げながら、積分したら良いです。
教科書には、デカルト座標と極座標の変換が例として出てるみたいです。
ちゃんと使いこなせるようになりたいところ!
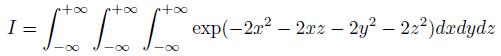


コメント