10/10の応用数学の授業から。
再び登場したわけですが、この授業が面白いんだー。
フーリエ級数の係数の求め方
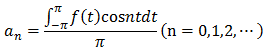
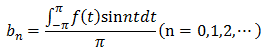
これを見ると、高校時代に学んだアレが思い浮かびます。
f(x)が偶関数の時
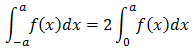
f(x)が奇関数の時
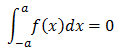
フーリエ級数の係数の積分は、ただのf(t)ではなく、それと三角関数の積の積分です。
だから、単純にf(t)の偶奇では場合分けできないかな・・・と思いきや!
余弦関数・正弦関数もそれぞれ偶関数・奇関数なので、話は単純にまとまります。
偶関数・奇関数の積は、偶関数になるのか奇関数になるのか。
結論は、こうです。
偶関数×偶関数=偶関数
偶関数×奇関数=奇関数
奇関数×偶関数=奇関数
奇関数×奇関数=偶関数
それは、偶数・奇数の積に置き換えて考えれば良いのかなと思ったら、違う。
偶数×偶数=偶数
偶数×奇数=偶数
奇数×偶数=偶数
奇数×奇数=奇数
冷静になって、偶関数・奇関数の定義まで戻ってみました。
f(x)が偶関数
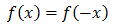
f(x)が奇関数
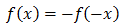
偶数・奇数という置き換えで考えるのではなく、正の数・負の数という置き換えで考えるべきのようです。
名前に騙されちゃいけない。
正×正=正
正×負=負
負×正=負
負×負=正
では、f(t)が偶関数か奇関数かで場合分けをします。
f(t)が偶関数のとき
偶関数cosntとの積は偶関数なので
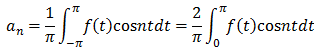
奇関数sinntとの積は奇関数なので
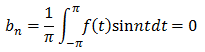
b=0、つまりsinの項が全て無くなり、f(t)はこのように表すことが出来ます。
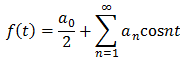
余弦関数の和で表されるので、これをフーリエ余弦級数と呼びます。
f(t)が奇関数のとき
偶関数cosntとの積は奇関数なので
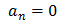
奇関数sinntとの積は偶関数なので
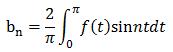
同じ発想で、こちらのf(t)はフーリエ正弦級数となります。
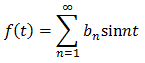
・・・で、綺麗に表せたから終わりか?
工学的には、積分を計算する量が半分に減ったわけです。
単純計算で半分の時間で同じ精度の解析ができます。
同じ時間をかければ、倍の精度の解析ができます。
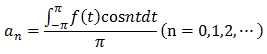

コメント