破産しない、簡単な方法があります。
使える資金のうちの一定比率を賭け続けるだけです。
少しずるいですが・・・。
たとえば「資金の1割を賭ける」と決めておきます。
資金が残り1ドルになったとき、「毎回1ドルを賭ける方針」では次に負けたら破産です。
固定比率の方針では、1割の0.1ドルしか賭けません。
だから破産しません。
残りの資金が0.01ドルになっても、賭け金を0.001ドルにするから破産しません。
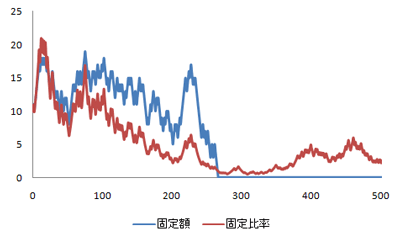
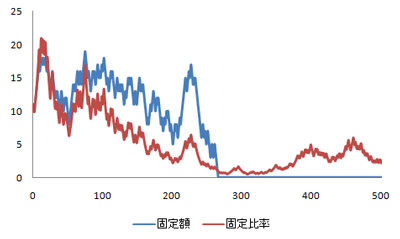
固定比率は、ギリギリのところで持ち直すかもしれません。
0.01ドルまで落ちたら、ほとんど破産しているのと一緒ですけど。
ただ、「ほとんど破産している」としても「破産しない」というのは大切です。
現実的な賭けは、十分な回数行って「大数の法則」が適用できるような状況にしなきゃなりません。
十分に大きい回数だけ賭けを実行すると「もの凄く小さい破産する確率」も結構大きくなります。
だから、破産する確率は「完全にゼロ」であることが大切なんです。
ところで、このグラフは利益の期待値がゼロの場合です。
期待値がゼロの賭けじゃ損をするばかりなので、ここからは期待値がプラスの場合を考えます。
なんとか期待値がプラスの賭けを見つけ出すんですよ!
まとめると、「期待値がプラスの賭けに資金のうちの固定比率を賭ける」というのが結論です。
「じゃあ、固定比率の比率ってどれくらい?」というのが次の問題です。
これは数学的に求められていて、「ケリー基準」と言います。
たとえば勝率60%でオッズ2倍の賭けに対する解は、比率20%です。
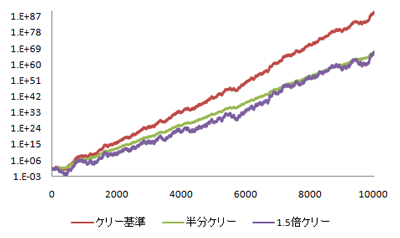
グラフの「半分ケリー」というのは、比率が小さめで10%の場合。
「1.5倍ケリー」は、比率が大きめで30%の場合です。
これを見ても分かる通り、ケリー基準が一番多くの利益を出しています。
そして、ケリー基準の半分の比率の場合と1.5倍の比率の場合の利益は長期的には等しいです。
これも数学的に証明されます。
ケリー基準は「期待値がプラスでない賭けはするな」ということも教えてくれます。
結局、ケリー基準を使うのが一番良さそうです。

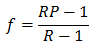
コメント