「母集団」なのか「標本」なのかって、あまり意識してないですよね?
母集団とは、想定している全てです。
標本は、その中からいくつかを取り出したものです。
たとえば、ニュースで内閣支持率なんてのが出たりします。
上がったとか下がったとかニュースで言っていますよね。
違うな、上がったってのは聞かないですね。
とにかく、あれを見てこう思った人はいませんか?
「おいらは支持するかどうかなんて聞かれていないのに、勝手に決めないでくれ!」
・・・と。
思わねーか。
内閣支持率に対する母集団は、日本の有権者全員。
標本は、その中からたまたま「支持しますか?」と聞かれた人です。
内閣支持率は、「有権者全員に聞いたら、こんな割合でした」みたいな雰囲気で発表されます。
つまり、「母集団の値」のように発表されます。
でも、実際には、ごく一部の人にしか質問していません。
実際に発表されているのは、「標本の値」です。
これがいわゆる標本詐欺です。
そんな言葉ないけど。
当然ですが、標本の統計量は、母集団の統計量とは一致しません。
ここから、統計学の言葉にします。
標本の平均を標本平均、母集団の平均を母平均と言います。
標本平均を母平均として扱うのには問題があります。
でも、実際にはそれをやっています。
これは「標本平均の平均」が母平均に一致するためです。
平均の平均なんて意味不明なので式にします。
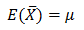
μは、母平均です。
Eというのは、平均という意味です。
期待値とも言います。
バー付きのXは、標本平均です。
定義を書くまでもないかもしれないけれど。
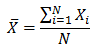
平均の平均とか意味不明ですが、この式が成立するから、発表される内閣支持率は「それほど間違ってない」と言えるのです。
ただし重ねて、母集団の値とは一致していないことを強調しておきます。
高校の数学で「平均」だけでなく「分散」も習いました。
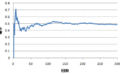
平均の場合と違って、「標本分散の平均」は「母分散」に一致しないから注意が必要です。
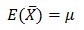

コメント
[…] 母集団 大数の法則 […]