ゆとり教育の話で有名な「円周率が3」について考察。
なぜ円周率が3だといけないのか。
円周率を3として求めた円周は、正6角形の周の長さに等しいです。
つまり、円を正6角形と近似しているようなものです。
・・・確かにその近似は不十分のような気もする。
過去の東大入試の「円周率が3.05より大きいことを示せ。」という問題。
これは、正8角形の周の長さを計算することで示すことができました。
逆に、円周率を3.05くらいとすれば、円を正8角形と近似しているようなもの。
円周率は一般的に3.14と近似されることが多いですが、これは十分なのか。
円周率を3.14と近似するのは円を正何角形と近似することなのか。
ここで、考察対象をひっくり返します。
正n角形の円周率はいくつになるのか。
・・・円周率という言い方は正しくないので、正多角形周率とでも呼ぶことにします。
たとえば、「正6角形周率は3」というわけですね。
正n角形周率の計算は難しくないです。
高校生の幾何で、以下の式が得られます。
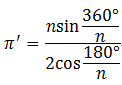
これを色んなnに対して計算してやります。
さて、正n角形周率が3.14となるnはいくつか。
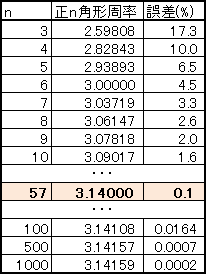
だいたい正57角形でした。
つまり、円周率を3.14と近似するということは、円を正57角形と近似するようなものです。
正57角形なら、確かにもう円といっても差支えないかな。
この表によれば、前述の東大入試は正8角形以上でしか示せないことも分かります。
正7角形では不十分なんですね。
ちなみに、正1000角形周率まで求めて表に載せたので参考にしてみてください。
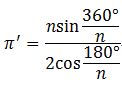


コメント