近似式が得られたところで、次は重み関数を考えます。
いきなりですが、今回使う重み関数を紹介します。
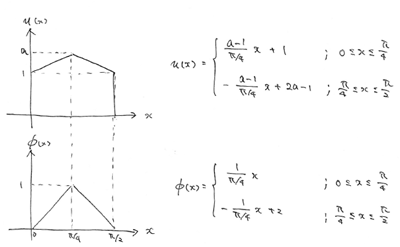
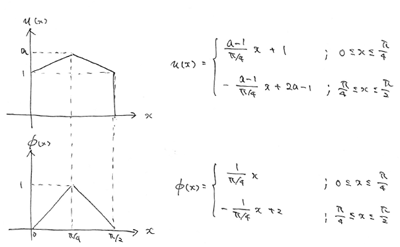
上が前回作った近似解。
下が今回設定した重み関数。
重み関数の条件としては、
・対象となる節点で1であること。
・それ以外の節点で0であること。
・全ての重み関数を足し合わせると、任意の点で1になることです。
最初の二つの条件については、グラフを見れば明らかです。
最後の条件については、グラフを見ても分からないです。
今回は節点が3つあります。
0とπ/4とπ/2です。
両端については境界条件で答えが出てるので考える必要ありません。
でも、両端にも重み関数があって、本当はそれを考慮する必要があります。
その重み関数も足し合わせると任意の点で1になります。
重み関数の理論とか、細かいことは置いておいて。
とりあえず、実際に計算してみることにします。
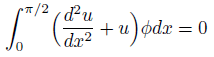
何を計算したら良いかと言えば。
解きたい偏微分方程式に、重み関数をかけたものでした。
このまま計算したら良いものですが、部分積分により少し展開します。
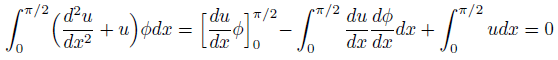
この必要性は不明。
そもそも不連続な関数を微分して良いのかが不明。
でも、これをしないと上手くいかない。
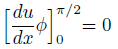
第1項はゼロになります。
なぜなら、重み関数は両端でゼロだからです。
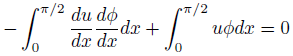
結局のところ、この式を解けば良いということになります。
aの姿が見えませんが、これはaについての方程式です。
というわけで、とりあえず近似式u(x)と重み関数φ(x)の微分を求める必要がありそうです。
どちらも線形な関数なんで、xの係数をとってくるだけですが。
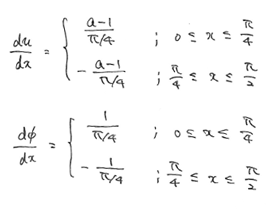
あとは、ぽいぽいぽいっと積分式に投げ込んで積分するだけです。
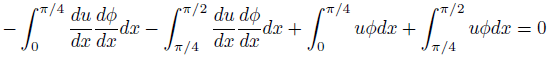
被積分関数は、要素ごとに定義されています。
そういうわけで、積分は要素ごとに分けて計算します。
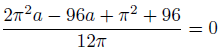
そして、計算した結果がこちら。
計算途中をだらだらと書いても仕方ないので省略。
多項式の積分なので、高校生でもできるはず!
そしてもう、aの一次方程式になっているので、簡単に解けます。
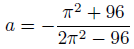
これを実際に数値にしてみると、1.3882・・・ってところです。
厳密解は2の平方根で、1.4142・・・です。
まあまあ。
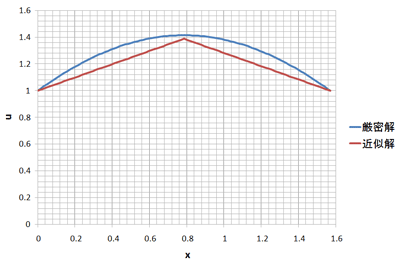
最後に厳密解と近似解をグラフで比較してみます。
節点が3つだけで、しかも線形という荒い近似でも、それらしい結果になりました。
精度を上げる方法は大きく分けて二通り。
・分割数を上げて、細かく計算する。
・直線でなく高次式で近似する。
ちなみに、今回は計算したい節点が1つでした。
だから、方程式は1本でした。
細かく分割すると、その数だけ方程式が出てきて、連立方程式になります。
実際に実用的な計算をしようと思うと、かなり巨大な連立方程式になります。
そして、その計算に、有限要素法の演算時間の大半をとられます。
ここまでで既に大変だけど、実際にはこの先がまた大変ということみたいです。
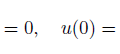

コメント