前回までの微分方程式は、「斉次形」といって、右辺が0でした。
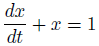
今回は、右辺を1とした「非斉次形」を扱います。
右辺が0でなければ「非斉次形」です。
斉次形というのは、イメージとしては入力のない微分方程式です。
たとえば、電源がない電気回路を微分方程式にすると、斉次形になります。
逆に、非斉次形は、入力がある微分方程式です。
この辺りは、微分方程式のラプラス変換をとった伝達関数を考えるとイメージしやすいかと思います。
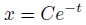
非斉次形の解を考えてみます。
まずは、試しに斉次形の一般解を代入してみます。
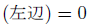
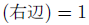
当たり前ですが、これらは一致しません。
だから、解になりません。
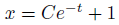
解に1という項を追加すれば、左辺も1になり解として成立します。
任意定数も含まれているので、これは一般解です。
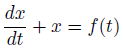
右辺が一般の場合を考えてみます。
積分因子をかけるという解法もありますが、ここでは「定数変化法」を用います。
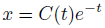
斉次形の一般解の定数係数を、関数と考えます。
そして、微分方程式に代入するだけ。
これだけのことで非斉次形の一般解が求められます。
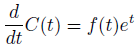
実際に代入してみると、途中の項がうまくキャンセルされます。
そして、係数の関数の微分方程式が得られます。
これは、いわゆる変数分離によって解くことができます。

このように変形できるので、f(t)次第では積分を実行できます。
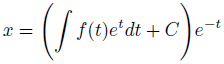
あとは、係数関数を元に戻せば一般解の出来上がりです。
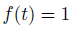
最初に挙げた微分方程式を、定数変化法で解きます。
右辺は1でした。
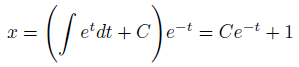
これを用いて計算すると、確かに先に得られたのと同じ一般解が得られます。
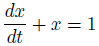
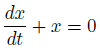
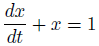
コメント