有限要素法でヘルムホルツ方程式を解いてみます。
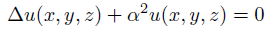
復習ですが、これがヘルムホルツ方程式。
変数自体と、その2階微分を含む微分方程式です。
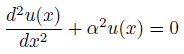
簡単にするために、1次元に落としました。
3次元の有限要素法を説明しようと思ったら、それこそ本になります。
有限要素法に使うのは、「近似解」と「重み関数」です。
近似解が欲しくて有限要素法を使おうとしているのに、近似解を要求されるなんて。
それは何故か?
まず、微分方程式じゃなくて、ただの方程式の数値解析法を思い出してみます。
分からないなら、エクセルのゴールシークを想像します。
それも分からないなら、電卓だけで方程式を解く方法を想像してみます。

まず、解はこれくらいかなっていう「適当な数値」を方程式に代入してみます。
答えがぴったりゼロになれば、それは厳密に方程式の解です。
そうでなければ、違う数値を入れてみて計算を繰り返します。
ぴったりでなくとも、0.0001くらいになれば、十分に良い近似解と言えます。

同様に、微分方程式を解くときも、まず「適当な近似解」を用意します。
それを微分方程式に代入してみて、0に近い値になれば解と認められます。
そういうわけで、まずは「とりあえずの近似解」を準備するわけです。
ただ、色々な近似解を代入して試してみるわけではありません。
定数を含む近似解を作って、その定数を定めることで、解を見つけ出します。
「色々な」の部分を、色々な数値に変化できる「定数」に肩代わりさせる様なイメージ。
そして、その定数の定め方がこれ。
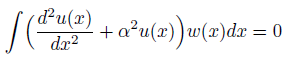
近似解に重み関数をかけて、領域積分し、ゼロと置く。
これを計算すると求めたい定数を含む方程式が得られます。
その方程式を解いて定数を定めれば解が得られる・・・というわけ。
さて、話は少し戻って、「重み付け残差法」の「残差」とは何か?
「とりあえずの近似解」を微分方程式に代入してみたらどうなるかといえば。
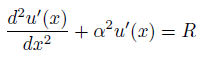
この式に限って、解u(x)が近似式であることを強調するために、ダッシュをつけています。
「とりあえずの近似解」が厳密解にぴったり一致していない限り、残差が残りますよね。
だから、残差です。
繰り返しになりますが、この残差を小さくするように、近似解中の定数を定めます。
その定め方は、重み関数をかけて、領域積分して、ゼロと置くことです。
これが重み付け残差法!
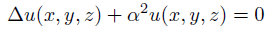

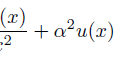
コメント