数学者が微分方程式を解くといえば、厳密解を求めることですが。
工学的には近似解が得られれば十分です。
解は関数になっている必要もなく、各点におけるサンプリングの結果だけで十分だったりもします。
とにかく近似的に解が得られれば十分なのだけど。
実際のところ微分方程式はどうやって解けば良いのか?

微分方程式の数値解析法としては、大きく分けて3種類あります。
最もシンプルなのが差分法で、これは数値解析の教科書なんかにちょろちょろっと書かれています。
対して有限要素法は、それだけで厚い教科書が書けてしまいます。
境界要素法については良く知らない。
有限要素法にも色々な流儀があるようです。
けれど、その根本にあるのは、ベルヌーイの考案した変分法という考え方です。
そして、今回勉強したのは、有限要素法の中の重み付け残差法です。
次の積分式を見てください。
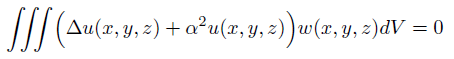
これが、微分方程式の数値解析法を記述しています。
しかも、差分法、有限要素法、境界要素法の全てを。
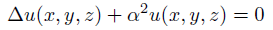
これは、ヘルムホルツ方程式という微分方程式です。
これを数値解析によって解こうとしているのが上の積分式です。
積分式の中にヘルムホルツ方程式の姿が見えます。
他の微分方程式を解きたい時は、その部分を変化させれば良いです。
上の積分式は、解きたい微分方程式に重み関数w(x,y,z)を書けて、領域積分して、ゼロと置いているだけ。
これで微分方程式が解けるということ。
重み関数として何を使うかによって、差分法、有限要素法、境界要素法が分かれます。
たぶん。
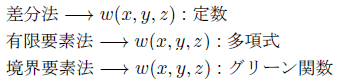
有限要素法の「重み付け残差法」の「重み付け」とはこの重み関数のこと。
「残差」というのは、積分式の中の「解きたい微分方程式を表す部分」です。
ざっと微分方程式の解法を俯瞰したところで、詳しい解説へ。


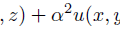
コメント