今日の小さな感動。
「重力とは、リーマン空間の曲がり具合である」
そもそも、リーマン空間ってなんだ、重力ってなんだって話です。
細かいことは良く分からないながら、分かったことをメモしておきます。
一般相対論的な運動方程式は以下のように表されます。
これは粒子に外力が働いていない場合の話です。
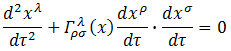
左辺第1項は、ニュートンの運動方程式でも現れる加速度の項です。
一般相対論で現れた第2項が、重力を表しています。
この第2項に現れるΓは、クリストッフェルの3指標数といって以下のように表されます。
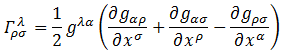
この計算については、参考文献の相対性理論の考え方を参照してください。
ともかく、Γは上のようにして求めることができます。
じゃあ、今度はgって何だって話になります。
これは計量テンソルといいます。
その定義式を書くとηという記号が出てきて、今度はηって何だって話になります。
ηは局所ローレンツ系における計量テンソルというらしいですが、もう意味不明です。
とにかく「η→g→Γ→重力」という感じで求められるわけですね。
重要なのは「g→重力」であるということです。
計量テンソルによって重力が定義されているということです。
さて、表題のリーマン空間とは何でしょう。
まず、4次元時空内の近接した2点間の微小距離dsを以下のように定義します。
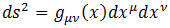
このdsが一般座標変換に対して不変に保たれる空間をリーマン空間といいます。
また、この空間で成立する幾何学をリーマン幾何学とか言います。
さて、上の微小距離dsの定義の中に、先ほどの計量テンソルgが出てきました。
こうして、「リーマン空間→g→重力」という結びつきが分かります。
結局、重力とはリーマン空間の曲がり具合であるということです。


コメント