有限要素法の手計算は、「2分割」の「1次要素」を用いて行いました。
そして前回は、「1次要素」のところは変えずに、分割数を上げて精度を向上させました。
今回は違うアプローチ。
「2分割」のところは変えずに、要素の次数を上げます。
次数を上げるということは、節点の間を2次関数とか3次関数で近似するということです。
高次要素を用いると、精度はどうなるのか?
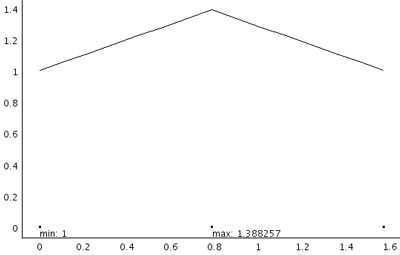
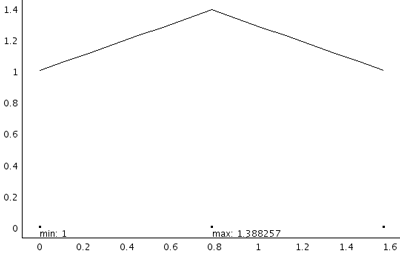
まず、1次要素です。
3回目の登場、相変わらず精度の悪さは否めない。
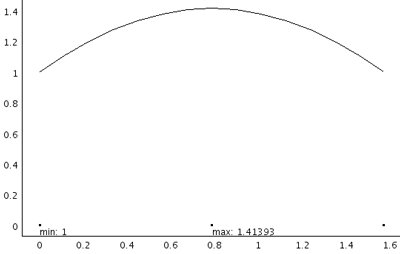
次数を一つ上げて、2次要素です。
あくまで2分割です。
左右の端と中間にだけ節点があって、その間を2次関数で近似する形。
曲線で近似するので、一気に厳密解に近づく印象です。
中間節点の値は、1.41393です。
1次要素を16分割した時の精度を既に超えています。
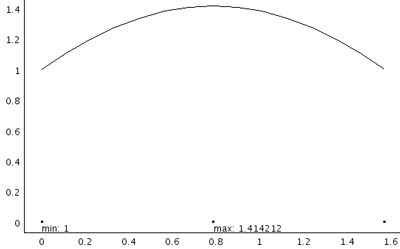
3次要素
中間節点の値は、1.414212。
もはや形状の違いは感覚では分からないので、数値に頼ります。
厳密解の中間の値は、1.41421356・・・です。
誤差1e-4%という低さ。
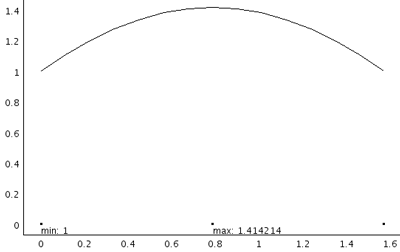
4次要素
中間節点の値は、1.414214で、もう表示桁数で精度が制限されるレベルです。
このように、分割数を上げたり高次要素を使うと、数値解の精度が向上します。
実際には両方を同時に用いて精度を上げます。
今回は高次要素に軍配が上がりましたが、次数をいくらでも上げられるというわけではありません。
実際、COMSOLで使える要素の最高次は5次で、これ以上は上げられません。
上げすぎると不安定になるという側面も持つからです。
逆に分割数はいくらでも上げられます。
こちらは上げれば上げるほど、単純に精度が上がります。
そういうわけで、ある程度高い次数の要素を設定し、あとは分割数によって精度を向上させる・・・というのが現実です。
コメント