微分方程式を解こう!
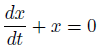
この微分方程式は、最大で1階微分が含まれているので、「1階微分方程式」です。
微分は偏微分でなく常微分なので、「常微分方程式」です。
最後に、線形性を持つので「線形微分方程式」です。
まとめると、「1階線形常微分方程式」といったところ。
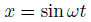
たとえば、三角関数が解になるんじゃないかと予想します。
定数ωを適切に定めれば解になるかも?
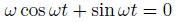
実際に代入して、tによらずこの式が成立するωを求めます。
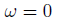
たとえば0なら、上の恒等式が成立します。
しかし、最初に戻ってみると、xが既に三角関数でなくなってしまうので、解ではありません。
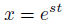
実は、指数関数が解になります。
今度は、定数sを適切に定めれば、これが解になるはずです。
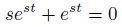
さきほどど同様に実際に代入してみます。
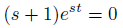
変形します。
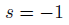
すると、定数sが得られます。
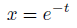
今度はしっかりと指数関数の形をとどめています。
これが解になります。
任意定数を1つも含まない解、つまり「特殊解」です。
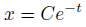
この解を定数倍しても解になります。
実際に代入してみたら解になることが分かります。
こちらは任意定数を1つ含むので、「一般解」です。
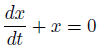


コメント