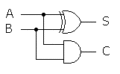
XORゲートをCMOSで作ってみます。
XORを基本ゲートに含むか、というのは微妙なところです。
というのも、XORはANDとORの組み合わせで作れるからです。
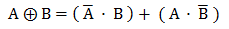
で、これをMOSFETで実現します。
一番単純な、上の式を素直に回路にした、完全相補形のロジック。
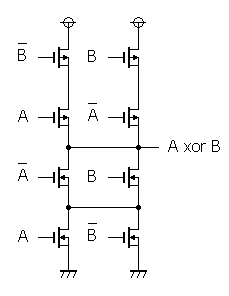
本当はデジタル的なMOSFETの記号を使いたいのだけど、あいにく手元のソフトに入っていない・・・。
と言っても、中心より上がpMOSで下がnMOSなので、簡単に分かります。
「完全相補形」というのは、pMOSの配置が完全にnMOSの鏡写しになっているものです。
鏡写しというのは、「直列は並列に、並列は直列に」という意味。
だから、下半分のnMOSだけを見れば良い。
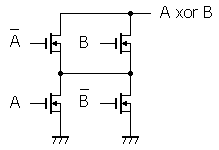
下半分にすると、電源が無くなります。
つまり、”1″にできなくなります。
グラウンドはあるから、”0″にはできます。
というわけで、「どんな時に”0″になるか」を考えて、nMOSを配置します。
“1”が入ったらnMOSがオンになるから・・・と考えれば、上の回路ができあがります。
・・・そんなこんなで、XORゲートは実現できます。
でも、これはトランジスタを8個も使っています。
AとBの否定を作らなきゃいけないことを考えると、12個のトランジスタが必要。
否定を作るのに2つずつのトランジスタが必要だから。
ちょっと工夫すれば、10個のトランジスタで完全相補形のXORゲートが作れます。
でも、そもそも完全相補形ではなく、他のロジックも色々あります。
ドミノロジックなんかが実際のLSIのチップには使われるみたいです。
簡単なのは、スイッチロジックというやつです。
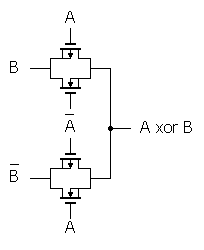
これなら、否定を作るためのトランジスタを合わせても、8個のトランジスタで済みます。
しかも、こちらの方が速かったりします。
もちろん短所もありますが。
これの見方を少し変えれば、3路スイッチの話ができます。
3路スイッチがXORゲートだという話をしましたが、それはまさにこの構造です。
MOSFETスイッチを壁にあるスイッチに置き換えれば、3路スイッチになるというわけ。
コメント