フェーザ法(4)

前回の復習から。

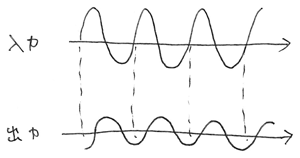
線形システムの定常解は、周波数そのまま。
振幅と位相だけが変わるのでした。

そして、その振幅と位相を求めたい。

しかし、フェーザ法の解といえば、複素数です。
複素数と、回路の出力波形の振幅と位相にどんな関係があるかといえば？

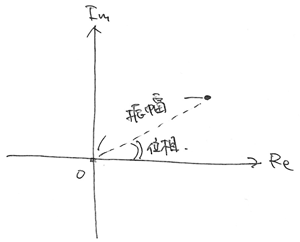
回路を解析したら、複素平面上のある点が得られます。
つまり、複素数が解として得られます。

その複素数の絶対値が、求めたかった振幅。
複素数の位相が、求めたかった位相。

ここまで分かったら、もうフェーザ法は分かったようなもんですね。

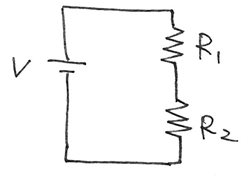
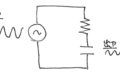
これは、中学生でも解ける回路です。
ただし扱っているのは、「実数」でした。

これを「複素数」に拡張したら、中学生と全く同じ手続きでもってコンデンサ付きの回路が解けます。
もちろん、解も複素数。
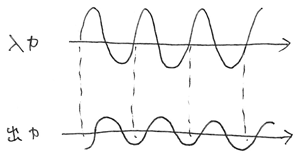
実際の出力波形は、その複素数の振幅と位相から分かります。

次、最後に実際に解いてみます。