ちょっと、ここいらで回路の入出力についてまとめておきます。
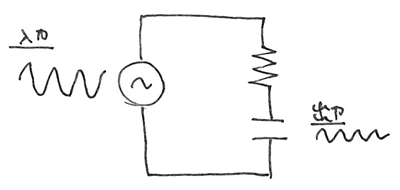
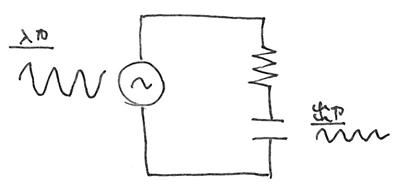
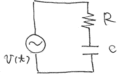
入力は、電源電圧で、正弦波としました。
出力は、コンデンサの両端の電圧で、定常状態で次のように得られました。
前回は、微分方程式の非斉次形の特殊解がどうのとか難しいこと言いましたが。
ここまでは、フェーザ法としては当然の前提です。
その理由を、正弦波と線形性から説明。
まず、正弦波。
正弦波には、3つの定数があって、それぞれが重要な特性を持っています。
Aは、振幅。
ωは、角周波数。
φは、位相。
次に、線形性。
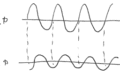
入力の波形が正弦波なら、出力の波形も正弦波になるのは、線形性から当然といえます。
では、入出力で何が変わるか?
角周波数は変わりません。
入力信号にない周波数成分が突然現れるというのは、線形システムではあり得ません。
それに対して、振幅と位相は変わります。
だから、フェーザ法で求めなければいけないのは、振幅と位相だけです。
入力が、
なら、出力は、
です。
入力が、
なら、出力は、
です。
ちなみに、次の2式は同じ意味です。
AとBを、Aとφに変換することができます。(AとAは別もの)
ここまでをまとめると、フェーザ法は「回路の定常状態における振幅と位相」を求める手法です。
コメント