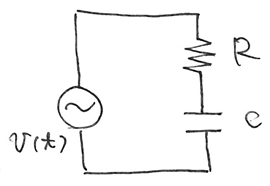
取り出しましたのは、RC直列回路。

これをフェーザ法を使って解いてみます。
何を求めるかといえば、コンデンサの両端にかかる電圧を求めます。
とは言っても、まずは普通に微分方程式を解いてみよう。
さくっと微分方程式を立てます。
分からない場合は、電気回路(2)を参照してください。
Vcはコンデンサの両端の電圧です。
v(t)は電源の電圧で、正弦波としましょう。
こういう微分方程式を解くときは、斉次形の一般解と、非斉次形の特殊解を足し合わせるのでした。
これは微分方程式の定石。
斉次形とは、
の形。
簡単だから、一般解が求められます。
非斉次形とは、
の形。
難しいけど、特殊解ならなんとか求められます。
「解を足し合わせる」というところで、勘の良い人は気付くと思いますが。
微分方程式の解は、斉次形の一般解と、非斉次形の特殊解の足し合わせ。
と同時に、過渡解と定常解の足し合わせでもありました。
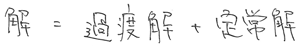
フェーザ法で求められる「定常解」というやつは、言い換えると「非斉次形の特殊解」です。
これ大事。
特殊解は、手当たり次第代入してみたら、見つかります。
試しに、
とか代入してみたら、これが特殊解になることが分かります。
定数は、あとで初期条件を代入して求めるのでした。
フェーザ法使っても、同じ解が得られます。
というか、フェーザ法を使えば、これの定数AとBが求められます。
続く。
コメント