 日記
日記 春休み終了
春休みのまとめ!これは、大学に入ってからの2年分。左から順に、16ヶ月分、6ヶ月分、2ヶ月分。・・・が、ほぼ同じ量になってしまうという不思議。そして、これが春休みに読破したテキストたち。春休みの勉強時間は、合計15,000分くらいでした。・...
 日記
日記  本
本  本
本  勉強
勉強  本
本  本
本  本
本 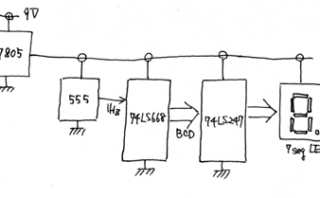 エレクトロニクス
エレクトロニクス  本
本  エレクトロニクス
エレクトロニクス