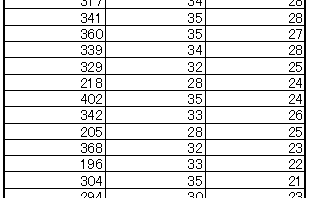
 勉強
勉強 重回帰分析
説明変数が1つの時は回帰分析でした。でも、このように説明変数が2つ以上ある場合は重回帰分析を使います。どちらも二乗誤差を最小にするという方法で求めます。最小二乗法ですね。説明変数が2つになると何がやっかいかと言えば、説明変数同士が依存しあっ...
 勉強
勉強 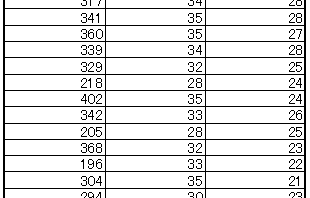 勉強
勉強 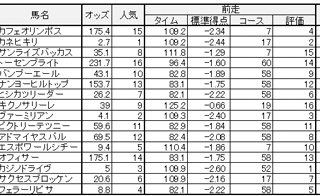 勉強
勉強 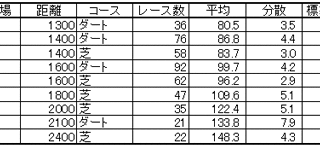 勉強
勉強 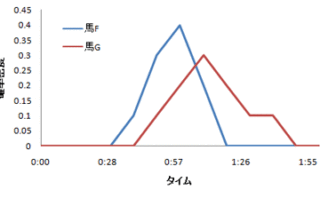 勉強
勉強 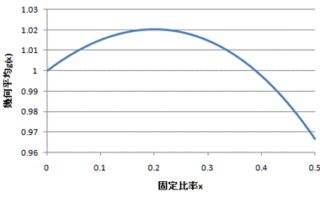 勉強
勉強 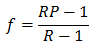 勉強
勉強 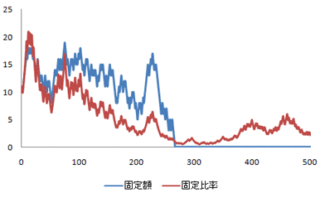 勉強
勉強  勉強
勉強 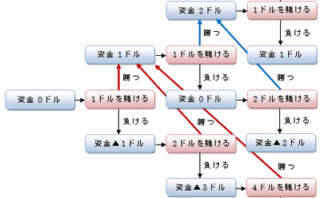 勉強
勉強