回路というやつは、電気系人間の最強の武器であると思います。
そこで、回路の素晴らしさを訴えていきたいと思います。
どんな物質でも良いのですが、とりあえず「アルミニウム」を取り上げます。
37.7MS/mという導電率を持つ金属です。
アルミニウムに電源を繋ぐとどうなるか?
これを考えようと思うと結構大変です。
もちろん電流が流れます。
すると磁界が発生します。
アルミニウムの中の電位は場所によって異なります。
そういうわけで、電界も生じます。
電源が交流だと、電流や電位、磁界や電界は、全て時間によって変化します。
アルミニウムがアンテナの役割をして電磁波を出したりもします。
電磁波を送信すれば受信もします。
アルミニウムから飛び出た電磁波が、またアルミニウムに入って・・・どうなるんだ?
訳が分からない。
これを解析する理論は、なんとびっくり、存在します。
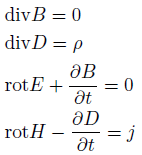
マクスウェル方程式です。
この4本の偏微分方程式を、3次元の空間で計算すれば解けます。
このAlの電気的なふるまいが分かるはずです。
ですが、この複雑な方程式の厳密な解を求めることは、まず出来ません。
アルミニウムの形がよほどシンプルな場合のみ。
そういうわけで代数計算は諦めるとして、数値計算なら解を求めることができます。
が、これはもちろん近似解に過ぎないし、その上に膨大な時間がかかる。
もちろん暗算や手計算は不可能です。
・・・そこで、「電気回路」の登場です。
回路という形にすれば、理系高校生でも解ける簡単な問題に早変わりします。
偏微分方程式が、常微分方程式になるだけで、計算の労力が劇的に減るということです。
簡単なものなら微分方程式ですらないただの連立方程式になり、中学生でも解けるような形になります。
もちろん厳密な答えではないのですが、工学的には十分。
精度にシビアな電気の世界もあるけれど、多くは結構アバウトでも扱えます。
ここまでは、系があって、そのふるまいを予想するという話でした。
逆に、「こんなふるまいをしてほしい」というのを元に回路を検討し、その系を作りだすということもできます。
いやー、回路って素晴らしい。
これから暇があれば、「回路」について詳しく書いていきたいと思います。

コメント