こちら、弟からの課題です。
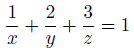
これを満たすx,y,zの整数解を求めるべし。
自然数という条件を勝手につけてしまったけれど、以下に解法。
整数問題をコンピュータに解かせるというのは、良い勉強になります。
#include
main(){
int x, y, z;
for( x = 2; 3*x*3 + 3*4 + 2*4*x >= x*3*4; x++ ) // xのループ
for( y = 3; 3*x*y + y*4 + 2*4*x >= x*y*4; y++ ) // yのループ
for( z = 4; 3*x*y + y*z + 2*z*x >= x*y*z; z++ ) // zのループ
if( 3*x*y + y*z + 2*z*x == x*y*z ) // 式を満たすか
printf( "(x, y, z) = (%d, %d, %d)n", x, y, z );
}
与式を次のように変形したのは、わたくしではありません。
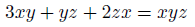
コンピュータに計算させることを考えると、小数計算をしなくて良いので大変有利。
計算機的な誤差も発生しないので良いです。
問題はどうやって有限の計算にするかということでした。
思考するときは先の式の方が考えやすいので、再び掲載。
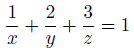
式の左辺は変数が大きくなると小さくなります。
それぞれの変数がある値より大きくなると、右辺が1を下回ります。
その時点で計算をやめてループを抜ければ良いという発想です。
計算結果がこちら。
(x, y, z) = (2, 5, 30)
(x, y, z) = (2, 6, 18)
(x, y, z) = (2, 7, 14)
(x, y, z) = (2, 8, 12)
(x, y, z) = (2, 10, 10)
(x, y, z) = (2, 12, 9)
(x, y, z) = (2, 16, 8)
(x, y, z) = (2, 28, 7)
(x, y, z) = (3, 4, 18)
(x, y, z) = (3, 6, 9)
(x, y, z) = (3, 12, 6)
(x, y, z) = (3, 30, 5)
(x, y, z) = (4, 3, 36)
(x, y, z) = (4, 4, 12)
(x, y, z) = (4, 8, 6)
(x, y, z) = (5, 4, 10)
(x, y, z) = (5, 10, 5)
(x, y, z) = (5, 40, 4)
(x, y, z) = (6, 3, 18)
(x, y, z) = (6, 4, 9)
(x, y, z) = (6, 6, 6)
(x, y, z) = (6, 24, 4)
(x, y, z) = (8, 4, 8)
(x, y, z) = (8, 16, 4)
(x, y, z) = (10, 5, 6)
(x, y, z) = (12, 3, 12)
(x, y, z) = (12, 12, 4)
(x, y, z) = (14, 4, 7)
(x, y, z) = (15, 6, 5)
(x, y, z) = (20, 10, 4)
(x, y, z) = (30, 3, 10)
(x, y, z) = (36, 9, 4)
それからそれから。
このプログラムが結構コンパクトにまとまっているのは、for文のおかげです。
whileで書こうと思ったら3~4倍くらいの行数になってしまう・・・。
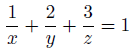


コメント