 勉強
勉強 偏相関係数
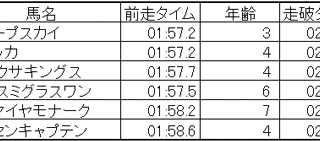
前走タイムだけでは、情報が足りなすぎる。そこで、年齢というデータを追加してみます。ここからが、回帰分析の面白いところ。少し難しいところでもあります。「前走タイム」と「年齢」という説明変数と、「走破タイム」という目的変数があります。その間の相...
 勉強
勉強  勉強
勉強  料理
料理 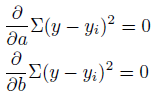 勉強
勉強 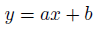 勉強
勉強 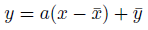 勉強
勉強 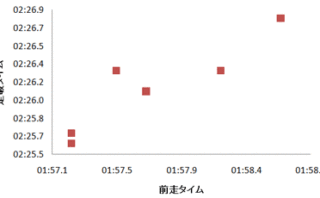 勉強
勉強  エレクトロニクス
エレクトロニクス 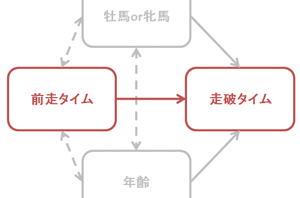 勉強
勉強